1. Геометрия
  2. Найдите радиус окружности

Найдите радиус окружности , вписанной в равнобедренный треугольник с основанием, равным 12 см, и боковой стороной , равной 10 см

olgalubnina201 olgalubnina201    1   20.01.2020 19:27    125

Ответы
вопрос65378 вопрос65378  11.10.2020 02:00
ответ:

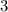3 см.

Объяснение:

Обозначим данный равнобедренный треугольник буквами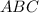 ABC.

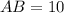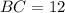Пусть AB = 10 см, BC=12 см.

=======================================================

Радиус вписанной окружности равнобедренного тр-ка находится по формуле:

R=\dfrac{BC}{2}\sqrt{\dfrac{2AB-BC}{2AB+BC}}

--------------------------------------------------------------------

\Rightarrow R=\dfrac{12}{2}\sqrt{\dfrac{2\cdot10-12}{2\cdot10+12}}=6\sqrt{\dfrac{8}{32}}=6\sqrt{\dfrac{1}{4}}=6\cdot\dfrac{1}{2}=\dfrac{6}{2}=3 см.


Найдите радиус окружности , вписанной в равнобедренный треугольник с основанием, равным 12 см, и бок
ПОКАЗАТЬ ОТВЕТЫ
Boss008Mta Boss008Mta  11.10.2020 02:00

решение представлено на фото

Объяснение:


Найдите радиус окружности , вписанной в равнобедренный треугольник с основанием, равным 12 см, и бок
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
прждлшеджж прждлшеджж  18.07.2019 00:00
Из точки вне плоскости проведены к ней две наклонные, каждая из которых образует с плоскостью угол в 45. определите расстояние от данной точки до данной плоскости, если...
olga0520 olga0520  18.07.2019 00:00
Одна сторона прямоугольника 20 см а диагональ 29 найти плошадь...
vadimfarxudinov vadimfarxudinov  18.07.2019 00:00
Впрямоугольном треугольнике abc из вершины прямого угла проведена высота ch. ab=48 см, ah=12 см. найдите ac....
IrishkaKoteika2689 IrishkaKoteika2689  18.07.2019 00:00
На боковых сторонах ав и вс равнобедренного треугольника авс отметили соответственно точки м и к так что угол вак равен углу всм докажите что вм равен вк...
vitalinaartikov vitalinaartikov  18.07.2019 00:00
Дакажите что трапеция вписанная в окружность всегда равнобокая,...
NastyaVelly NastyaVelly  18.07.2019 00:00
Найдите площадь круга и длину, ограничивающей его окружности, если диаметр равен 14 см....
wasuablezko wasuablezko  18.07.2019 00:00
Если все вершины многоугольника лежат на окружности то окружность называется?...
verka000 verka000  18.07.2019 00:00
Сторона ас треугольника авс проходит через центр описанной около него окружности найдите угол с,если угол а =24...
darya1122334455667 darya1122334455667  18.07.2019 00:00
Основою прямої призми є трикутник, сторони якого 5 см, 5 см, 6 см. висота призми дорівнює більшій висоті цього трикутника. знайдіть об єм призми....
новичок625 новичок625  18.07.2019 00:10
Впрямоугольном ∆abc(с= 90) проведена высота сн. найдите вн, если ас=12 см, ан = 6 см....

Популярные вопросы