Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 15 и 5 корней из 7. .
Ответы
По теореме Пифагора диагональ он же диаметр окружности равен 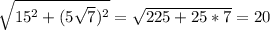 тогда радиус равен половине то есть
тогда радиус равен половине то есть 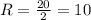
ПОКАЗАТЬ ОТВЕТЫ
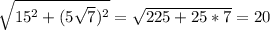 тогда радиус равен половине то есть
тогда радиус равен половине то есть 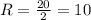
Радиус окружности, описанной около прямоугольника, равен половине диагонали, потому что вписанный прямой угол всегда опирается на диаметр описанной окружности. Проведём любую диагональ, получим 2 прямоугольных треугольника с катетами 15 и 5 корень из 7. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, поэтому 15^2+(5корень из 7)^2=225+175=400, диагональ = квадратный корень из 400=20. Радиус = половине диаметра, поэтому R=20:2=10
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Выполните умножение b(a-3+c)=...
2 - Проаналізуйте етапи здобуття незалежності України (1990-1991 рр.) До ть...
3 - Чотирикутник abcd вписано в коло .Знайти кут d і кут a, якщо кут b дорівнює 27...
2 - 1. Постройте контраргументацию к следующим рассуждениям: а) Если на демонстрацию,...
2 - Обозначьте причастные и деепричастные обороты, расставьте знаки препинания, составьте...
3 - КесипСүрөттө кайсы кесиптин ээлери? Алар жөнүндө маалыматты таблицагажазгыла....
3 - Legal systems So far we’ve explored some of the history and development of the...
3 - Значение химии в жизни человека. Хемофилия и хемофобия. Современная химия и экологические...
2 - Чем отличаются бунты и восстание второй половины XVII века от событий Смутного...
1 - Просто ответьте что то рандомное для балов!...
1