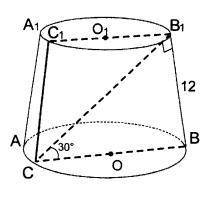
Найдите радиус меньшего основания усеченного конуса

Давайте разберемся с этой задачей.

Усеченный конус - это конус, у которого отрезан верхний участок. В данной задаче у нас есть картинка, на которой изображен усеченный конус.

Для нахождения радиуса меньшего основания усеченного конуса нам потребуется знание о свойствах подобных фигур.

Подобные фигуры имеют одинаковую форму, но разные размеры. Для нахождения радиуса меньшего основания нам нужно использовать свойство подобных фигур.

На картинке усеченного конуса видно, что имеется две окружности - большая и меньшая. Для обозначения и отличия их радиусов обозначим радиус большей окружности как R, а радиус меньшей окружности как r.

Теперь, посмотрим на структуру конуса.

У нас есть два треугольника: ABC и ADE. Треугольник ABC - это внешний треугольник, а треугольник ADE - это внутренний треугольник.

Обратите внимание, что треугольники ABC и ADE подобны, так как у них есть два равных угла и они имеют одинаковое соотношение сторон.

Теперь мы можем использовать это свойство подобных фигур для нахождения радиуса меньшей окружности.

Мы можем воспользоваться формулой, которая гласит:
(R - r) / R = DE / AC

Здесь AC - это высота конуса, DE - это высота усеченного конуса. Обратите внимание, что DE будет равно разности высот конусов AD и AE. То есть:
DE = AD - AE

Решим задачу шаг за шагом:

1. Определим длины сторон треугольника ABC и ADE.
Мы можем использовать изображение для определения значений этих сторон.
По изображению, сторона AC равна высоте конуса и равна 12 см.
Сторона AD равна радиусу большей окружности и равна 9 см.

2. Найдем высоту усеченного конуса.
Высота усеченного конуса будет равна разности высот конусов AD и AE.
В задаче не указана высота конуса AE, но мы можем сказать, что высота AE меньше, чем высота AC (12 см), так как AE находится ниже.
Давайте в качестве примера примем, что AE = 6 см.

3. Подставим полученные значения в формулу.
(R - r) / R = DE / AC
(9 - r) / 9 = (9 - 6) / 12

Теперь мы можем решить эту пропорцию.
Необходимо найти значение r.

(9 - r) / 9 = 3 / 12
Умножим обе части пропорции на 12.
12(9 - r) = 9 * 3

Распространим скобки и упростим:
108 - 12r = 27

Теперь выразим r:
-12r = 27 - 108
-12r = -81
r = (-81) / (-12)
r = 6.75 см

Ответ: Радиус меньшего основания усеченного конуса равен 6.75 см.