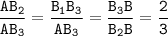Найдите пропорциональные отрезки, отношение которых равно как: а) 1 б) 2: 3 тут дробь
Другие вопросы по теме Геометрия
Популярные вопросы
- Как были связаны между собой кочевой быт и культура казахов? + примеры...
3 - Зробіть висновок про вплив забруднення повітря на рослину...
3 - Подчеркни слова, в которых нет звука й: мясо, дядя ,юля, ключ, вьюга?...
2 - Периметр равнобедренного треугольника abc равен 84дм а боковая сторона...
2 - Как было устроено государством в древнем китае...
2 - Напишите окончания быздын сендердын сездердын олардын...
3 - Найдите неизвестный член пропорции 2/2/3: 3/1/3=x: 3,5...
2 - написать эссе на тему: дорога к счастью...
1 - Подчеркни не проверяемые ударением.уторм мы пришли в лес.ветерок...
2 - Ядро ізотопу торію th 232 90 зазнає альфа розпаду.яке ядро утворюється...
1
AA₁=A₁A₂=A₂A₃=A₃A₄=A₄A₅ поэтому AB₁=B₁B₂=B₂B₃=B₃B₄=B₄B по теореме Фалеса.
А) Отрезки, которые относятся как 1, равны.
Отношение любых двух отрезков из AB₁ , B₁B₂ , B₂B₃ , B₃B₄ и B₄B равно 1.
Например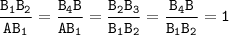
Б) Отрезки с отношение . Один отрезок должен состоять из двух частей, а другой из трёх, при этом все части равны.
. Один отрезок должен состоять из двух частей, а другой из трёх, при этом все части равны.
(AB₂ или B₁B₃ или B₂B₄ или B₃B) и (AB₃ или B₁B₄ или B₂B)
Вариантов множество выбираем два отрезка из первой скобки и второй. Получаем отрезки, отношение которых 2 к 3.
Например