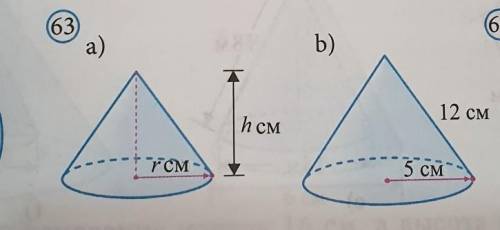
Найдите полную поверхность и объём конуса на рисунке .

Для нахождения полной поверхности и объема конуса на данном рисунке, нам понадобится знание основных формул для конуса.

Начнем с нахождения полной поверхности конуса.

Полная поверхность конуса состоит из двух частей: боковой поверхности и основания.

Боковая поверхность конуса представляет собой образующую конуса, свернутую вдоль окружности основания. Поэтому, чтобы найти площадь боковой поверхности, нужно умножить длину отрезка, соединяющего вершину конуса с центром основания, на окружность основания.

Длина образующей можно найти с помощью теоремы Пифагора, примененной к прямоугольному треугольнику, образованному образующей, радиусом и высотой конуса.
Давайте обозначим образующую как l. Величина, которая равна половине основания, является основанием площади. Поэтому, основание составляет половину диаметра основания, а это радиус расстояния OD.

Теперь найдем высоту конуса. Для этого воспользуемся теоремой Пифагора в прямоугольном треугольнике, образованном диаметром основания и радиусом. Выстраиваем прямоугольный треугольник: OD — прямой угол. По теореме Пифагора находим высоту (расстояние от вершины конуса до плоскости основания).

Затем, найдем окружность основания конуса. Для этого нужно знать радиус основания. Отметим, что в данной задаче у нас дана площадь основания, а не радиус.

Таким образом, если мы знаем образующую, высоту и площадь основания, можем найти все параметры конуса и его полную поверхность с помощью соответствующих формул.

Для нахождения объема конуса на данном рисунке, нужно использовать формулу:

V = (1/3) * S * h, где V - объем конуса, S - площадь основания, h - высота конуса.

Теперь, зная формулы, приступим к вычислениям:

1. Найдем образующую l.
l = √(r² + h²)
l = √(6² + 8²)
l = √(36 + 64)
l = √100
l = 10

2. Найдем высоту h:
h = √(l² - r²)
h = √(10² - 6²)
h = √(100 - 36)
h = √64
h = 8

3. Найдем радиус основания r:
S = πr² = 36
πr² = 36
r² = 36 / π
r = √(36 / π)
r ≈ √11.46
r ≈ 3.39

4. Найдем площадь основания S:
S = πr²
S = π(3.39)²
S ≈ π(11.46)
S ≈ 35.97

Теперь, когда у нас есть все необходимые значения, мы можем рассчитать полную поверхность и объём конуса.

1. Полная поверхность конуса:
Полная поверхность = площадь основания + площадь боковой поверхности
Полная поверхность = S + πrl
Полная поверхность = 35.97 + π(3.39)(10)
Полная поверхность ≈ 35.97 + 106.95
Полная поверхность ≈ 142.92

2. Объем конуса:
V = (1/3) * S * h
V = (1/3) * 35.97 * 8
V ≈ (11.99)(8)
V ≈ 95.92

Таким образом, полная поверхность конуса на данном рисунке составляет приблизительно 142.92 единиц квадратных, а объем конуса равен приблизительно 95.92 единицам кубического объема.