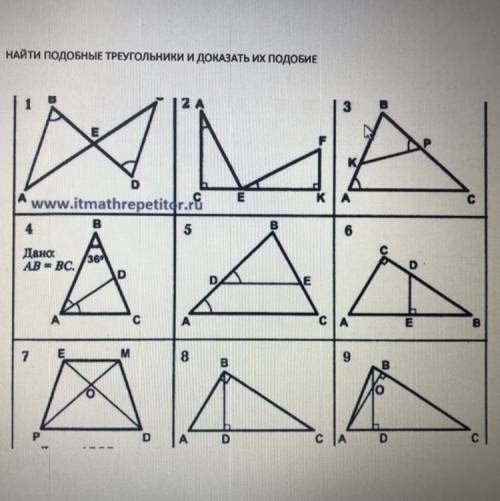
Найдите подобные треугольники и докажите их подобие
Другие вопросы по теме Геометрия
Популярные вопросы
- Трудности и преодоления васютки таблица из рассказа васюткино озеро...
3 - Главные герои и идея произведения симонова живые и мёртые...
1 - Решите квадратное неравенство -x²-4x+5≥0...
3 - Обратите внимание на то, что, хотя роман толстого посвящен войне и...
3 - Решите 1. полидактилия – доминантный аутосомный признак. гомозиготы...
3 - Прямая проходит через точку (0; 3) параллельно оси ох напиши формулу...
1 - Назови орфограммы, объясни графические правописания слов. расскажу,...
1 - 3/5 части сливок состовляет малсло сколько процентов сливок состовляет...
1 - Какие процессы приводят к уменьшению энергии световой волны при прохождении...
1 - Стаблицей эволюционные и революционные изменения! максимум ....
2
Для нахождения подобных треугольников, мы должны сравнить их стороны и углы.
Первый треугольник имеет стороны длиной 13 см, 5 см и 12 см, а второй треугольник имеет стороны длиной 6,5 см, 2,5 см и 6 см.
1. Проверка соотношения сторон:
Для того чтобы треугольники были подобными, их стороны должны быть пропорциональны. Для этого мы сравниваем длины двух пар сторон.
Сравним стороны AB и DE. Соотношение длин сторон AB/DE = 13/6,5 = 2.
Затем сравним стороны BC и EF. Соотношение длин сторон BC/EF = 5/2,5 = 2.
И, наконец, сравним стороны AC и DF. Соотношение длин сторон AC/DF = 12/6 = 2.
Мы видим, что соотношение длин сторон в обоих треугольниках равно 2. Значит, стороны треугольников пропорциональны, что является одним из условий для подобия треугольников.
2. Проверка соотношения углов:
Для того чтобы треугольники были подобными, их углы должны быть равны или пропорциональны.
Мы видим, что треугольники имеют одинаковый угол B, который находится между сторонами BC и AB.
Также треугольники имеют одинаковый угол E, который находится между сторонами EF и DE.
И, наконец, треугольники имеют одинаковый угол C, который находится между сторонами BC и AC.
Мы видим, что треугольники имеют одинаковые углы, что также является одним из условий для подобия треугольников.
Таким образом, основываясь на соотношениях сторон и углов, мы можем сделать вывод, что данные треугольники являются подобными.