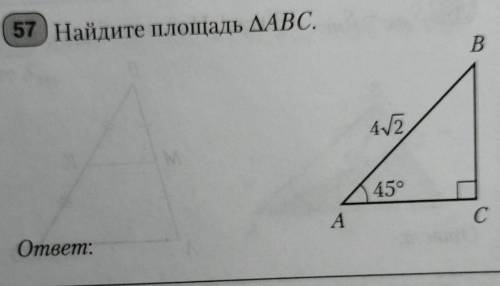
Найдите площади АВС. АВ- 4корень из 2. А - 45°

Объяснение:

чтобы найти площадь используем формулу S=1/2ab

тогда найдем неизвестные стороны используя теорему синусов

ВС/sin45=4√2/sin90

BC=4√2/sin90×sin45

BC=4√2×√2/2

BC=4 см

теперь найдем и вторую сторону, так как один из двух углов 45, это равнобедренный треугольник, следовательно ВС тоже 4 см

посчитаем площадь:

S=1/2×4×4

D=2×4

S=8 см²

8ед²

Объяснение:

∆АВС- равнобедренный треугольник

<С=90°; <А=45°; <В=45°. Углы при основании равны.

АС=ВС.

Пусть сторона АС будет х, тогда сторона ВС тоже будет х.

Из теоремы Пифагора

АС²+ВС²=АВ²

Составляем уравнение:

х²+х²=(4√2)²

2х²=32

х²=16

х=√16

х=4

АС=4ед; ВС=4ед.

Площадь прямоугольного треугольника равна половине произведения двух катетов.

S(∆АВС)=AC*BC/2=4*4/2=16/2=8ед²