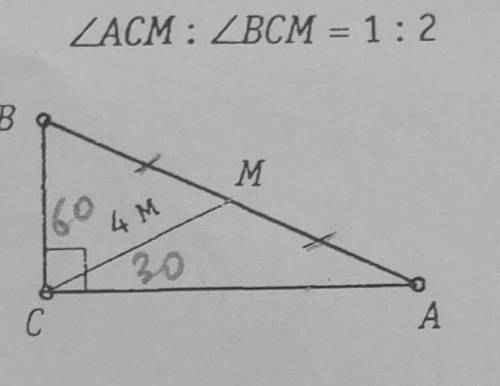
Найдите площадь треугольника. угол АСМ: углу ВСМ=1 : 2​

Для решения этой задачи мы можем использовать формулу для площади треугольника: S = 0.5 * a * b * sin(C), где a и b - длины сторон треугольника, С - угол между этими сторонами.

В данной задаче у нас известны длины сторон АМ и BM, а также отношение угла АСМ к углу ВСМ, равное 1:2. Для начала мы должны найти углы треугольника АМВ.

Угол ВАМ можно найти, используя формулу прямоугольного треугольника:
tan(ВАМ) = (AM / BM)
tan(ВАМ) = (6 / 8)
ВАМ = arctan(6 / 8)
ВАМ ≈ 36.87°

Угол АВМ = 180° - (ВАМ + ВСМ)
Угол АВМ = 180° - (36.87° + 2 * 36.87°)
Угол АВМ = 180° - (36.87° + 73.74°)
Угол АВМ = 180° - 110.61°
Угол АВМ ≈ 69.39°

Теперь мы можем использовать формулу для площади треугольника, чтобы найти S.
S = 0.5 * AM * BM * sin(ВСМ)

Но у нас есть проблема: нам не дан размер стороны СМ, которую мы использовали для нахождения угла ВСМ. Давайте предположим, что сторона СМ равна 1.

Теперь мы можем найти длины сторон АС и ВС, используя пропорции.
Длина стороны ВС = (BM / Sin(ВАМ)) * Sin(АВМ)
Длина стороны ВС = (8 / Sin(36.87°)) * Sin(69.39°)
Длина стороны ВС ≈ (8 / 0.598) * 0.936
Длина стороны ВС ≈ 12.71

Длина стороны АС = СМ + СВ
Длина стороны АС = 1 + 12.71
Длина стороны АС ≈ 13.71

Теперь мы можем использовать формулу для нахождения площади треугольника:
S = 0.5 * АС * ВМ * Sin(ВСМ)
S = 0.5 * 13.71 * 8 * Sin(1 : 2)
S ≈ 0.5 * 13.71 * 8 * Sin(0.5)
S ≈ 0.5 * 13.71 * 8 * 0.479
S ≈ 41.71

Итак, площадь треугольника составляет примерно 41.71 квадратных единиц.