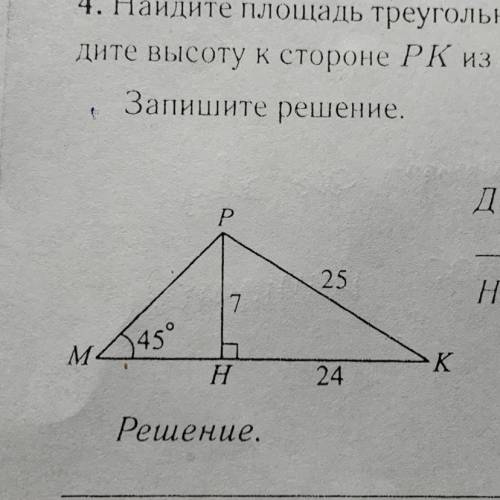
Найдите площадь треугольника МРК, используя данные рисунка. Прове- дите высоту к стороне РК из точки М. Найдите её длину.
Запишите решение.

Хорошо, давайте рассмотрим данную задачу и найдем площадь треугольника МРК. 1. Для начала обратимся к самому треугольнику МРК на рисунке. По определению, чтобы найти площадь треугольника, необходимо знать длины двух его сторон и между ними угол. Однако в данной задаче у нас даны только две стороны: МР и РК. Поэтому мы не можем применить прямую формулу для нахождения площади треугольника. 2. Однако, в задаче также просится провести высоту к стороне РК из точки М. Высота - это отрезок, который проходит через вершину треугольника и перпендикулярен к одной из его сторон. Когда мы проведем высоту, треугольник будет разделен на два прямоугольных треугольника: МРА и МАК. 3. Теперь необходимо вычислить длину высоты. Для этого можно воспользоваться теоремой Пифагора в прямоугольном треугольнике МАК. По теореме Пифагора мы знаем, что квадрат гипотенузы (в данном случае длина стороны МК) равен сумме квадратов катетов. Так как мы ищем длину катета - высоты треугольника МРК, то можем записать уравнение: МК^2 = МА^2 + АК^2 4. Для нахождения МА и АК мы можем воспользоваться свойствами прямоугольных треугольников. В треугольнике МРК угол МРК является прямым, поэтому угол МРА тоже является прямым. Таким образом, МРА также является прямым треугольником. 5. По свойству прямоугольных треугольников МРК и МРА, сторона МА будет являться катетом треугольника МРА, а сторона МР будет гипотенузой. АК будет соответственно другим катетом треугольника МРА. 6. В задаче даны данные для нахождения стороны МР (гипотенузы). Из рисунка видно, что МН = 120. Также нам дано, что NR = 80. Тогда для нахождения МР можем воспользоваться теоремой Пифагора: МР^2 = МН^2 + NR^2 МР^2 = 120^2 + 80^2 МР^2 = 14400 + 6400 = 20800 МР ≈ √20800 = 144.28 Теперь у нас есть значение МР, которое позволяет найти МА и АК через соответствующие соотношения: МА = МР * sin(МАК) АК = МР * cos(МАК) 7. Для этого нам нужно знать величину угла МАК. Но данная информация не предоставляется в задаче, поэтому мы не сможем точно определить значения МА и АК. 8. Таким образом, невозможно точно найти длину высоты треугольника МРК и, соответственно, найти его площадь. Важно понимать, что в задачах геометрии может быть много исключительных случаев, где задача не будет иметь однозначного решения или будет невозможно найти все необходимые данные. В данной задаче именно такой случай - длина высоты и площадь треугольника МРК невозможно найти без дополнительных данных.