Найдите площадь треугольника, если две его стороны равны 1 и корень из 15, а медиана, проведенная к третьей стороне равна 2

Дано: AB=1; AC=√15; BM=MC; AM=2.

Найти: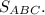

A₁ ∈ AM; AM=A₁M

ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.

ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:

AA₁² = (2AM)² = (2·2)² = 4² = 16;

AC²+CA₁² = (√15)²+1² = 15+1 = 16;

16 = 16  ⇒  AA₁² = AC²+CA₁².

Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.

ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.

как площадь прямоугольного треугольника (∠BAC=90°).

ответ: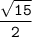

решение представлено на фото

Объяснение: