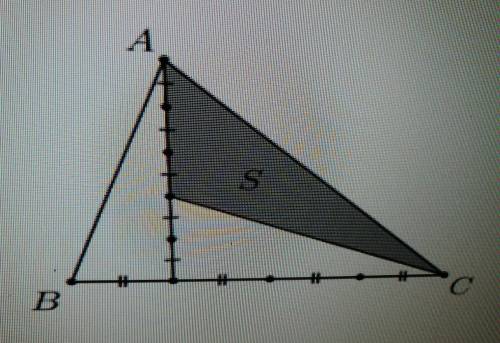
Найдите площадь треугольника abc, если s = 18 (s - площадь серого треугольника)

Добрый день! Давайте решим вместе задачу по нахождению площади треугольника abc.

Изображение показывает треугольник abc, а также серый треугольник. Обозначим стороны треугольника abc как a, b и c, а высоту, опущенную на сторону a, как h.

Мы знаем, что площадь серого треугольника равна 18 и обозначим ее как s.

Формула для нахождения площади треугольника abc через стороны и высоту выглядит так:
S = (1/2) * a * h.

Для нахождения площади треугольника нам нужно выразить сторону a через известные значения.

Обратим внимание на треугольник abc. Мы видим, что он разделен серой линией на два треугольника, один из которых - треугольник abc, а второй - меньший треугольник aed.

Треугольники abc и aed являются подобными, поскольку у них соответствующие углы равны (угол abc равен углу aed, поскольку они соответствуют вертикальным углам, и угол cba равен углу aed, поскольку они являются вписанными углами над хордой ac).

Поэтому стороны треугольников пропорциональны:
(a / ae) = (c / cd).

Мы знаем, что сторона а равна сумме сторон ae и ed:
a = ae + ed.

Подставим это в стороночную пропорцию:
(ae + ed / ae) = (c / cd).

Так как мы знаем, что cd равно 2 (поскольку серый треугольник является трапецией с боковыми сторонами, равными друг другу), мы можем записать уравнение в виде:
(ae + ed / ae) = (c / 2).

Решим это уравнение относительно ae и ed:
ae + ed = (c / 2) * ae.

Перенесем всё в одну сторону:
ae - (c / 2) * ae = -ed.

Приведем правую часть уравнения к общему знаменателю:
ae - (c * ae / 2) = -ed * 2 / 2.

Домножим обе части уравнения на 2:
2ae - c * ae = -2ed.

Теперь объединим подобные члены:
ae(2 - c) = -2ed.

Используя симметрию, заметим, что -2ed равно площади серого треугольника s.
Тогда наше уравнение примет вид:
ae(2 - c) = -2s.

Мы знаем, что s равно 18, поэтому:
ae(2 - c) = -2 * 18,
ae(2 - c) = -36.

Также нам дано, что s равно половине площади треугольника abc:
s = (1/2) * a * h.

Подставим это в уравнение:
(1/2) * a * h = 18,
a * h = 36.

Теперь выразим h через a:
h = 36 / a.

Таким образом, у нас есть два уравнения:
ae(2 - c) = -36,
h = 36 / a.

Используя эти уравнения, мы можем найти площадь треугольника abc.

Подставим значение h в формулу площади треугольника:
S = (1/2) * a * h,
S = (1/2) * a * (36 / a).

Упростим выражение:
S = 18.

Таким образом, мы получили, что площадь треугольника abc равна 18.