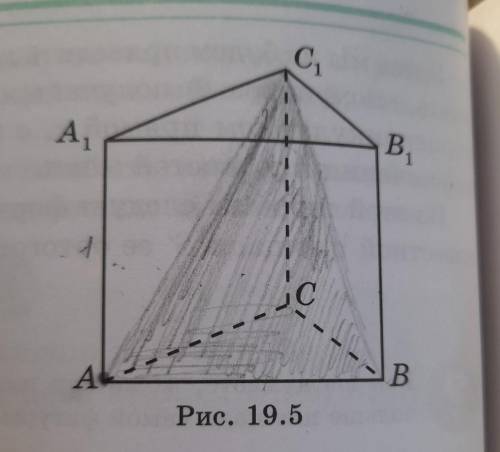
Найдите площадь сечения правильной треугольной призмы АВСА1В1С1 , все ребра которой равны 1 , плоскостью, проходящей через вершины А , В и С1 (рис

Хорошо, давайте по порядку решим эту задачу.

Сначала давайте проанализируем задачу. Нам дана правильная треугольная призма АВСА1В1С1, где все ребра равны 1. И нам нужно найти площадь сечения этой призмы плоскостью, проходящей через вершины А, В и С1.

Для начала вспомним, что сечение треугольной призмы будет также треугольником. Поскольку сечение происходит плоскостью, проходящей через вершины А, В и С1, то это будет треугольник, образованный сторонами призмы, проходящими через эти точки.

Теперь давайте посмотрим, какие стороны призмы проходят через вершины А, В и С1. Мы видим, что стороны, которые проходят через вершины А и С1, равны 1, так как все ребра призмы равны 1.

Следовательно, стороны треугольника в сечении призмы АВСА1В1С1, проходящей через вершины А, В и С1, будут равны 1 и 1.

Так как это правильная треугольная призма, то сторона BC также равна 1, так как все ребра равны 1.

Теперь давайте посчитаем площадь этого треугольника в сечении. Для этого мы можем использовать формулу площади треугольника, которая гласит:

Площадь треугольника = (основание * высота) / 2.

Основание - это одна из сторон треугольника в сечении, а высота - это расстояние от этой стороны до противоположного угла треугольника.

В нашем случае, одна сторона треугольника в сечении равна 1, а вторая сторона (между вершинами А и С1) также равна 1.

Теперь найдем высоту треугольника. Обратите внимание, что стороны АВ и ВС1 образуют прямой угол. Поэтому высота треугольника будет равна расстоянию между этими двумя сторонами.

Мы можем использовать теорему Пифагора для нахождения этого расстояния.

Вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В нашем случае, катеты АВ и ВС1 равны 1, так как все ребра призмы равны 1.

Подставим значения катетов в формулу Пифагора:

1^2 + 1^2 = гипотенуза^2.

1 + 1 = гипотенуза^2.

2 = гипотенуза^2.

Теперь найдем гипотенузу, извлекая корень из обеих сторон:

√2 = гипотенуза.

Таким образом, высота треугольника в сечении равна √2.

Теперь мы можем использовать формулу для нахождения площади треугольника:

Площадь треугольника = (основание * высота) / 2.

В нашем случае, основание равно 1, а высота равна √2.

Подставим значения в формулу:

Площадь треугольника = (1 * √2) / 2.

Упростим выражение:

Площадь треугольника = √2 / 2.

Таким образом, площадь сечения правильной треугольной призмы АВСА1В1С1, все ребра которой равны 1, плоскостью, проходящей через вершины А, В и С1, равна √2 / 2.

Ответ: площадь сечения равна √2 / 2.