Найдите площадь ромба с углом в 30 градусов, если площадь круга, вписанного в него равна 10пи.
Другие вопросы по теме Геометрия
Популярные вопросы
- Надо придумать словосочетаний с этими словами: baby,babies, glass,glasses,box,boxes,dish,dishes,shelf,shelves...
1 - Расставьте знаки препинания: он хотел уверить себя что никакой опасности...
1 - Разделите цепочку на шесть фраз....
3 - Зимой в нашей зоне большинство растений не фотосинтезируют и кислород...
1 - Решите уравнение. : з (оно должно быть квадратное.) 2x+1+109=x(x+1)...
3 - Придумать короткую смешную новогодную сказку...
2 - Латунь-сплав меди с цинком,причем цинк и медь входят в него в соотношении...
1 - Есть 66яблок и 33 яблока их разложтли в коробки по 3кг сколько понадобится...
2 - Напишите письмо своим родителям о своем доме и о своих занятиях...
3 - Навстречу друг другу направились асет и арслан .скорость асета 62 м/...
3
Есть в данном случае две формулы для вычисления площади ромба
Первая формула.
В данном случае полупериметр ромба равен 2а, где а - сторона ромба.
Формула принимает вид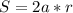
Найдем радиус круга. Площадь круга равна
Значит формула приобретает вид
Другая (вторая) формула исходит из формулы параллелограмма
Приравняем правые части формулы
Умножим обе части на 2
Сократим обе части на а.
Или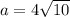
Подставим в формулу
S=80 - площадь ромба
ответ: 80 - квадратных единиц площадь ромба.
пл р=сторона на высоту =а*h
пл кр=10пи=пи r^2 из пл круга выразим его радиус
радиус=корень из 10
диаметр=2*радиуса=2*корень из 10
сторона против 30 гр = половине гипотенезы значит сторона ромба равна 4* корень из 10
отсюда найдем пл ромба
s=4* корень из 10*2 * корень из 10=80
ответ 80