Найдите площадь правильного четырёхугольника, если радиус его описанной окружности равен 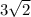
Другие вопросы по теме Геометрия
Популярные вопросы
- Мына жумбакты шешуге комектес. Келиннен кайын атасынын аты ким...
1 - A) What is the name of Aigul’s new project? b) What is the Guinness...
2 - ответьте кто знает!! Вроде по телеканалу карусель показывали такой...
1 - Реши задачу. Рабочие на детской площадке сделали клумбу прямоугольной...
2 - Народ мені розв язок необхідно терміново. Хімічний склад винної...
2 - У Буратино есть много монет по 4 и по 7 сольдо, каждого вида более...
2 - Кто приходить до пузиря хазяїн з якого метою...
2 - Что было бы если наша страна распологалась на вершинах гор...
3 - 1. Особенности становления и развития мирового философского процесса...
2 - Какова строение почки у тополя...
1
Для начала, давайте вспомним, что такое правильный четырехугольник. Правильный четырехугольник — это четырехугольник, у которого все стороны равны между собой, а все углы также равны.
В данной задаче нам дано значение радиуса описанной окружности, которая вписана в правильный четырехугольник. Обозначим радиус этой окружности как R. Из условия задачи, дано, что R = 3√2.
Площадь правильного четырехугольника можно найти с помощью следующей формулы: S = R^2 * sin(360°/n), где S - площадь, R - радиус описанной окружности, n - количество сторон правильного четырехугольника.
В нашем случае, количество сторон правильного четырехугольника равно 4, так как это четырехугольник. Подставим значения в формулу и найдем площадь:
S = (3√2)^2 * sin(360°/4)
Сначала рассмотрим sin(360°/4). Заметим, что sin(360°/4) = sin(90°) = 1. Так как sin(90°) равен 1, то оставим просто 1 вместо sin(360°/4).
Теперь, продолжаем вычисления:
S = (3√2)^2 * 1
= 9 * 2
= 18
Таким образом, площадь правильного четырехугольника равна 18.
Надеюсь, ответ был понятен! Если есть еще вопросы или что-то не ясно, пожалуйста, спросите. Я всегда готов помочь!