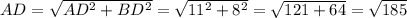Найдите площадь параллелограмма если его диагональ равна 11 см, перпендикулярно стороне равной 8 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Путешествие Гуллевера. Найти значение непонятных, трудных слов. ...
1 - Установить, какое из предложений (первое или второе) является следствием...
3 - Найбільши глибини знаходяться в районі Індія...
3 - Какими украинцы и белорусы от тяжелыхусловий жизни?Невыплачивали налогиУходили...
2 - Размер торговой пошлины, которую взимал Медведь заввозимые в Осиновую Рощу...
3 - НУЖНО Запишите уравнения возможных реакций. (а) NaOH + SO3 → (b) H2SO4 +...
2 - Read and complete with the verbs in the Past Simple.In a country far away...
2 - 1)6000зменш на 2сотні. 2) Знайди периметр квадрата, якщо його сторона 18...
2 - Мәтінді тыңда. Түсінгеніңді баянда. Мәтін бойынша жоспар құра....
3 - 2. Найдите наибольшее и наименьшее значение функции на данном промежутке:...
3
Объяснение:
Так как BD перпендикулярно AB, то угол ABD = 90 градусов. Рассмотрим треугольник BAD.По теореме Пифагора