1. Геометрия
  2. Найдите площадь параллелограмма

Найдите площадь параллелограмма ABCD, если BC=18 см, CD=5 см, угол A=30° ​

rakhmanets rakhmanets    3   18.11.2020 16:04    28

Ответы
botanchik1 botanchik1  18.12.2020 16:07

Дано :

Четырёхугольник ABCD - параллелограмм.

BC = 18 см, CD = 5 см, ∠А = 30°.

Найти :

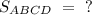
S_{ABCD} ~=~?

Противоположные углы параллелограмма равны.

Следовательно, ∠А = ∠С = 30°.

Площадь параллелограмма равна произведению его смежных сторон и синуса угла между ними.

Следовательно,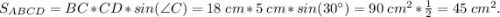 S_{ABCD} =BC*CD*sin(\angle C) = 18~cm*5~cm*sin(30^{\circ} ) = 90~cm^{2} *\frac{1}{2} = 45~cm^{2} .

45 см².


Найдите площадь параллелограмма ABCD, если BC=18 см, CD=5 см, угол A=30° ​
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
nikolya5 nikolya5  11.08.2019 20:40
Найдите площадь прямоугольного треугольника если его катеты равны 21 см и 34 см...
madmiss madmiss  11.08.2019 20:40
Найдите периметр ромба abcd, если его диагональ bd равна 8 см, а угол b равен 120 градусов...
аня2933 аня2933  16.07.2019 01:40
Впрямоугольном треугольние гипотенуза равна c а один из острых углов равен а найдите второй острый угол и катеты...
susovaanastasia susovaanastasia  16.07.2019 01:40
Треугольник со сторонами 10,12,15 остроугольный?...
jsjdnnx jsjdnnx  15.07.2019 10:40
Вравнобедренном треугольнике cdf с основанием cd угол c = 66 .найдите смежный угол при вершине д...
susannashakiro susannashakiro  15.07.2019 10:40
Верно ли утверждения? 1)внешний угол параллелограмма равен одному из внутренних углов 2)существует треугольник со сторонами 2,корень из 2,и3.5 3)квадрат вписанный в круг занимает маньше...
rada1213 rada1213  04.04.2019 20:30
Две параллельный прямые пересекаются секущей в точках a и b. прямая ab составляет с одной из параллельных прямых угол 30°. расстояние между этими параллельными прямыми равно 8,5 см....
Anny505 Anny505  04.04.2019 20:29
проволочной сеткой длиной 600 м нужно оградить участок земли прямоугольной формы. при каких рзмирах участки ее площадь будет наибольшей...
AlenaStypak AlenaStypak  04.04.2019 20:27
Площа прямокутника дорівнює 96 см2 . одна з його сторін у 6 разів більша ніж друга . знайдіть меншу сторону прямокутника . ​...
zdjby1 zdjby1  04.04.2019 20:25
Решите . все треугольники прямоугольные. 1)bc=4см sin=1/3 ac,ab - ? 2) ab=2см ctga=3 ac,bc - ?...

Популярные вопросы