1. Геометрия
  2. Найдите площадь фигуры ,ограниченной

Найдите площадь фигуры ,ограниченной линиями y=x^2+4,x=0,x=3 и y=0

SeamCard SeamCard    3   25.05.2019 17:50    0

Ответы
Fleksander Fleksander  21.06.2020 23:21
Фигура является криволинейной трапецией, ее площадь находим по формуле 
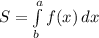
S= \int\limits^a_b {f(x)} \, dx
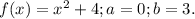
f(x)=x^2+4; a=0;b=3.
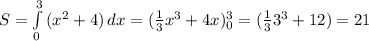
S= \int\limits^3_0{(x^2+4)}\,dx=(\frac{1}{3}x^3+4x)^3_0=(\frac{1}{3}3^3+12)=21
ПОКАЗАТЬ ОТВЕТЫ
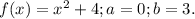
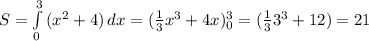
Другие вопросы по теме Геометрия
AlicaWolker16 AlicaWolker16  25.05.2019 23:10
Что такое метод доказательства от противного...
oldespower oldespower  25.05.2019 23:10
Начертите два неколлинеарных вектора a и b. постройте векторы равные 1)1/2a+3b. 2)2b-a....
ilya7klass ilya7klass  25.05.2019 23:10
Вравно бедренной трапеции диагональ является биссектрисой угла при основании. большее основание трапеции равно 26 см, а периметр - 50 см. найти меньшее основание трапеции....
ЕваКимСокДжин ЕваКимСокДжин  25.05.2019 23:10
De средняя линия треугольника abc найти стороны если ad= 3 см de=5 см, ce= 6 см !...
Liza14102004 Liza14102004  25.05.2019 23:10
Треугольник мнк задан своими координатами м(-6,1) н(-2,4) к(2,-2) докажите,что треугольник равнобедренный,найти высоту проведённую из вершины м. 4.написать уравнение прямой проходящ....
anettaaa1 anettaaa1  21.05.2020 13:26
треугольник ABC вписан в окружность Найдите Угол A и угол B этого треугольника если угол C= 35° дуга AC=60°...
odarka1596 odarka1596  21.05.2020 13:25
решить даю все былы что есть сделать нужно до 14:30​...
theknow14 theknow14  31.05.2019 13:02
Сторона основи правильної чотирикутної піраміди рівна 6 см , а бічне ребно 13 см. знайти об єм піраміди...
ВетаКлойзен54 ВетаКлойзен54  31.05.2019 13:13
1) один из углов треугольника равен 57°,а второй равен 44°,найти третий угол. 2) найти угол смежный с углом авс, если авс равен 111°. 3)найти углы равнобедренного треугольника,если...
mvrlin mvrlin  31.05.2019 15:50
Периметр правильного шестиугольника описанного около окружности равен 6 корней из 3 найти радиус этой окружности...

Популярные вопросы