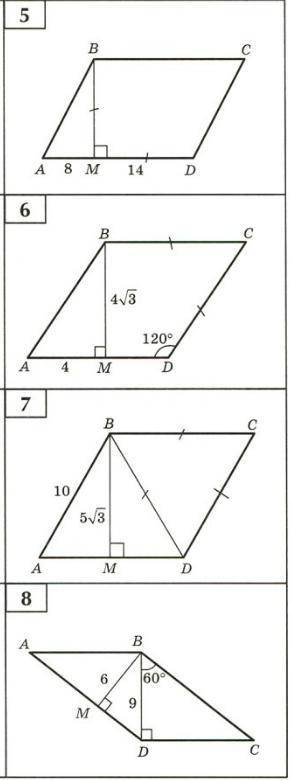
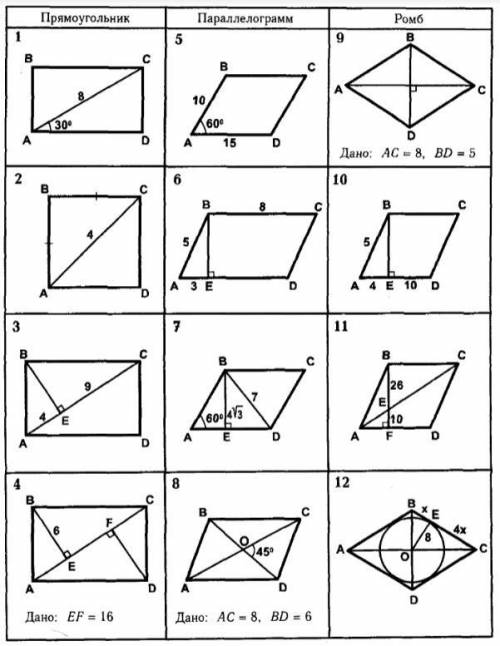
Найдите площадь данных параллелограммов и ромбов

Для нахождения площади параллелограмма необходимо умножить длину одной из его сторон на высоту, опущенную на эту сторону.

Для первого параллелограмма:
1. Мы видим, что даны сторона (a) и высота (h).
2. Найдем площадь (S) параллелограмма, используя формулу S = a * h.
3. Подставим значения: S = 8 см * 4 см = 32 см².
Таким образом, площадь первого параллелограмма равна 32 квадратным сантиметрам.

Для второго параллелограмма:
1. Здесь также даны сторона (a) и высота (h).
2. Найдем площадь (S) параллелограмма, используя формулу S = a * h.
3. Подставим значения: S = 12 мм * 7 мм = 84 мм².
Таким образом, площадь второго параллелограмма равна 84 квадратным миллиметрам.

Теперь перейдем к ромбам.

Для первого ромба:
1. В данном случае дано значение одной из диагоналей (d1 = 8 см).
2. Найдем площадь (S) ромба, используя формулу S = (d1 * d2) / 2, где d2 - другая диагональ ромба.
3. Значение d2 отсутствует на заданной диаграмме, поэтому нам необходимо его найти.
4. Заметим, что диагонали ромба делят его на четыре равных треугольника.
5. Каждый из этих треугольников - равнобедренный, так как две его стороны равны соответствующим сторонам других треугольников.
6. Используем теорему Пифагора для нахождения значения второй диагонали.
a^2 + b^2 = c^2, где a = 4 см (половина диагонали ромба), b = 6 см (высота ромба, опущенная на один из его углов), c - значение второй диагонали.
4^2 + 6^2 = c^2
16 + 36 = c^2
52 = c^2
c = √52
c ≈ 7.21 см (округлим до двух десятичных знаков)
7. Теперь, зная обе диагонали (d1 = 8 см и d2 ≈ 7.21 см), найдем площадь ромба: S = (8 см * 7.21 см) / 2 ≈ 28.84 см².
Таким образом, площадь первого ромба составляет около 28.84 квадратных сантиметра.

Для второго ромба:
1. В данном случае дано значение одной из диагоналей (d1 = 9 см).
2. Найдем площадь (S) ромба, используя формулу S = (d1 * d2) / 2, где d2 - другая диагональ ромба.
3. Значение d2 отсутствует на заданной диаграмме, поэтому нам необходимо его найти.
4. Заметим, что диагонали ромба делят его на четыре равных треугольника.
5. Каждый из этих треугольников - равнобедренный, так как две его стороны равны соответствующим сторонам других треугольников.
6. Используем теорему Пифагора для нахождения значения второй диагонали.
a^2 + b^2 = c^2, где a = 4 см (половина диагонали ромба), b = 7 см (высота ромба, опущенная на один из его углов), c - значение второй диагонали.
4^2 + 7^2 = c^2
16 + 49 = c^2
65 = c^2
c = √65
c ≈ 8.06 см (округлим до двух десятичных знаков)
7. Теперь, зная обе диагонали (d1 = 9 см и d2 ≈ 8.06 см), найдем площадь ромба: S = (9 см * 8.06 см) / 2 ≈ 36.27 см².
Таким образом, площадь второго ромба составляет около 36.27 квадратных сантиметров.

Окончательно:
1. Площадь первого параллелограмма равна 32 квадратным сантиметрам.
2. Площадь второго параллелограмма равна 84 квадратным миллиметрам.
3. Площадь первого ромба составляет около 28.84 квадратных сантиметра.
4. Площадь второго ромба составляет около 36.27 квадратных сантиметров.