1. Геометрия
  2. Найдите периметр треугольника,

Найдите периметр треугольника, вершины которого расположены в точках А (1; 2; 3 ), В ( 2; 3; 1)?

pashkevich00 pashkevich00    3   27.09.2020 11:26    13

Ответы
zhahbota zhahbota  27.09.2020 12:01

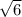
P=3\sqrt{6}

Объяснение:

стороны находятся по формуле: АВ=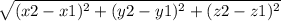\sqrt{(x2-x1)^{2}+(y2-y1)^{2}+(z2-z1)^{2} }

x1 y1 z1=координаты 1ой точки в стороне х2 у2 z2=координатывторой точки в стороне

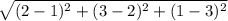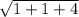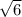
АВ=\sqrt{(2-1)^{2}+(3-2)^{2}+(1-3)^{2}}=\sqrt{1+1+4}=\sqrt{6}

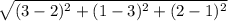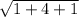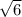
BC=\sqrt{(3-2)^2+(1-3)^2+(2-1)^2}=\sqrt{1+4+1}=\sqrt{6}

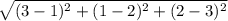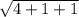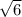
AC=\sqrt{(3-1)^2+(1-2)^2+(2-3)^2}=\sqrt{4+1+1}=\sqrt{6}

треугольник равнобедренный ------>P=3a=3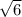\sqrt{6}

примечание:ты не дал значение С поэтому я дал тот С который был у меня в учебнике

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
efr47 efr47  23.12.2020 10:56
Висота паралелограма зі стороною утворюе кут 18°. Обчисли тупий кут паралелограма...
fedorovufa fedorovufa  23.12.2020 10:56
Геометрия. Найти сторону BC. Наверно нужно сделать при теоремы синусов. 9 класс....
milkivey3 milkivey3  23.12.2020 10:56
с геометришей, и не просто ответы, а с решением...
supervalad supervalad  23.12.2020 10:56
Дан шестиугольник ABCDEF, у которого все стороны и углы равны. Вершины A, C, E соединены отрезками. Чему равна градусная мера угла ACE, если ∠EAC = 60° ? ответ: ∠ACE = ....
deonisius03 deonisius03  23.12.2020 10:56
Площадь двух подобных треугольников составляет 55м2 и 220м2. Если одна сторона второго треугольника равна 10м, найдите длину стороны первого треугольника, соответствующей этой...
Ramazan1403 Ramazan1403  23.12.2020 10:57
Угол АВC = 28°. При гомотетии с коэффициентом, равным 2, угол АВС переходит в угол А1В1С1. Найдите величину угла А1В1С1 *​...
iuhagng iuhagng  23.12.2020 10:57
По какому признаку два треугольника равны? Выбери признаки соответственно изображениям. Первый признакВторой признакпТретий признак​...
затура56 затура56  23.12.2020 10:58
Найдите cosα, tgα, сtgα если sinα =4/9...
saaashaaa4656 saaashaaa4656  23.12.2020 10:58
16 номер: найти х. Доказать почему используется теорема Пифагора....
fox363 fox363  23.12.2020 10:58
Abcd трапеция bc угол 4 см,высота Ce2/3 Ad 60⁰уголнайдите Ad​...

Популярные вопросы