Найдите периметр треугольника с площадью 6√3 см ² и углом 60°, если стороны,прилежащие к данному углу, относятся как 3: 8
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. 2x-(8-x)+(3x-2)=6x-102. (x+3)(x-3)=x+3(x-3)...
2 - Порядок прилагательных: Поставьте прилагательные в правильном порядке....
1 - 1). Кем является Микеланджело Буонарроти?2).Допиши названия его скульптур:...
1 - Дати коротку характеристику зовнішньої політики Європейського Союзу наприкінці...
3 - номера 3, 5 и 7 Хотя бы что знаете...
1 - Составить мини рассказ о любом рабочем органе машин технология...
1 - Сочинение моя любимая конфета тофифи 30-40 слов на эстонском...
1 - Разделить число а на число b – это значит найти такое число x, которое......
1 - Немецкий язык 6 упражнение...
2 - Разделить число а на число b – это значит найти такое число x, которое......
3
Объяснение:
Обозначим данный треугольник буквами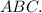
======================================================
Пусть - часть стороны, тогда
- часть стороны, тогда 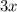 - AC, а
- AC, а 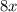 - AB.
- AB.
Но так как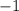 - отрицательное, значит оно не подходит.
- отрицательное, значит оно не подходит.
По теореме косинусов найдём CB: