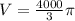Найдите объем шара,если площадь сечения его плоскостью, удаленной от центра шара на расстояние 6м,равна 64pi м^2
Другие вопросы по теме Геометрия
Популярные вопросы
- Мәтін мазмұны бойынша 2 проблемалық сұрақ құрастырыңыз. ...
3 - ОТВЕТЬТЕ БЫСТРЕЕ, ДАС : К хорде СД, центр которой равен радиусу окружности...
3 - Сколько лет было Чингизхану когда он умер? быстрее...
3 - Вопрос № 1. Дополните фразу: « Часть Вооруженных Сил государства, предназначенная...
2 - сторона прямоугольника Ad на 12 см больше чем сторона Cd,когда Ad увеличили...
1 - -3х²=5,7хРешите по программе 8 класса....
2 - 4. Начертите окружность радиуса 3см. с центром О.Проведите луч с началом...
3 - .. ฅ^•ﻌ•^ฅмне самой не очень видно, но у кого было?Кто может ?(...
1 - переказати розділ роману Чорної ради де розповідається найбільше про чорну...
3 - Колесо радіусом 5 см обертається так що залежність кута повороту радіуса...
2
Площадь сечения = πr²
r=√(S/π)=√(64π/π)=8
По т Пифагора найдем радиус шара
R²=r²+h²
R=√(8²+6²)=10
V=4/3 *πR³=4/3*π*10³=4000π/3
Так как сечение шара есть окружность, зная ее площадь найдем радиус:
Тогда исходя из прямоугольного треугольника во вложении находим радуис сферы:
Тогда объем сферы равен:
ответ: