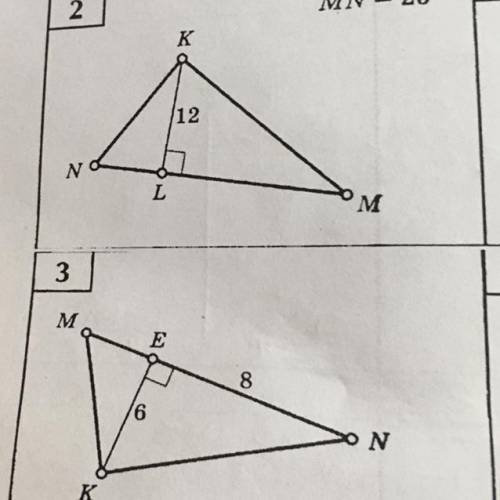
Найдите неизвестные элементы треугольников (угол K=90*) в номере 2 MN=25

Для решения данной задачи мы можем использовать теорему Пифагора, так как в треугольнике АМК прямой угол K = 90 градусов.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы (сторона, противолежащая прямому углу) равен сумме квадратов катетов (остальных двух сторон треугольника).
В данной задаче имеется треугольник АМК, где сторона AM является гипотенузой.
Из задачи известно, что сторона MN равна 25.

Шаг 1: Найдем длину стороны АК.
Используя теорему Пифагора, мы можем записать уравнение: АМ^2 = АК^2 + КМ^2.

Заменяя значения, получим: АК^2 = АМ^2 - КМ^2.
Так как АМ = 25 и КМ = 7, то: АК^2 = 25^2 - 7^2.
Вычисляя: АК^2 = 625 - 49 = 576.
Чтобы найти АК, возможно взять квадратный корень из обеих сторон: АК = √576 = 24.

Шаг 2: Найдем длину стороны КМ.
Так как мы уже нашли длину стороны АК, мы можем использовать теорему Пифагора, чтобы найти длину стороны КМ.
Используем уравнение: КМ^2 = АМ^2 - АК^2.
Заменяя значения: КМ^2 = 25^2 - 24^2.
Вычисляя: КМ^2 = 625 - 576 = 49.
Чтобы найти КМ, возможно взять квадратный корень из обеих сторон: КМ = √49 = 7.

Таким образом, после выполнения всех шагов, мы определили, что сторона АК равна 24, а сторона КМ равна 7.