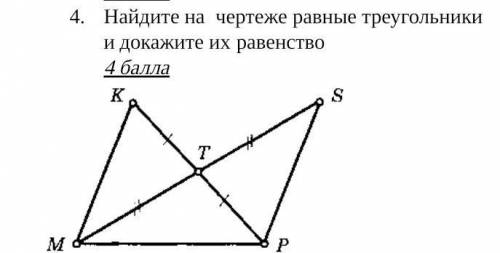
Найдите на чертеже равные треугольники и докажите их равенство
Другие вопросы по теме Геометрия
Популярные вопросы
- только правильно а то банан училка влепит номер 10 можете писать просто цифры я...
1 - СДЕЛАЙ ПРЕДЛОЖЕНИЕ В будущем времени,обращая внимания на структуру предложения(+/-/?)...
1 - Сын есімге 10 мысал (сөйлем керек)...
3 - Поясніть, чому при з берега за наближенням корабля ми бачимо спочатку верхівку,...
3 - расположите структуры по мере их удаления от оси тела. 1. трицепс (трехглавая мышца...
2 - Галина Ильина профессия ветров Опиши это явление природы...
2 - Почему бунин в рассказе Кавказ пишет так много про любовь и так мало про их расстование...
1 - Теңдеуді шеш. х - 1,5/3 = 6...
1 - Кто такой Солон, когда стал архонтом. Суть закона Основное содержание...
2 - 1. Какова роль дыхания для человека? Думаю об этом ответ 2. Почему вам нужна респираторная...
3
Для доказательства равенства двух треугольников необходимо, чтобы у них были равными соответствующие стороны и равными соответствующие углы.
В треугольнике АВС у нас все стороны равны: АВ=АМ, ВС=МН и АС=НС. Здесь мы можем использовать уже имеющуюся информацию о прямоугольнике АВС. В прямоугольнике противоположные стороны равны, поэтому АВ=СМ и ВС=СА. Тогда можно утверждать, что АМ=НС, то есть стороны треугольников АВС и АМН равны.
Кроме того, треугольник АВС имеет два прямых угла в точках В и С, а треугольник АМН также имеет два прямых угла в точках М и Н. Это значит, что углы В и М, а также углы С и Н являются прямыми углами. Следовательно, углы В и М, а также углы С и Н равны между собой.
Таким образом, у треугольников АВС и АМН равны соответствующие стороны и равны соответствующие углы, что доказывает их равенство.
Необходимо отметить, что для доказательства равенства двух треугольников иногда требуется использовать другие свойства и теоремы, но в данном случае достаточно информации, приведенной выше.