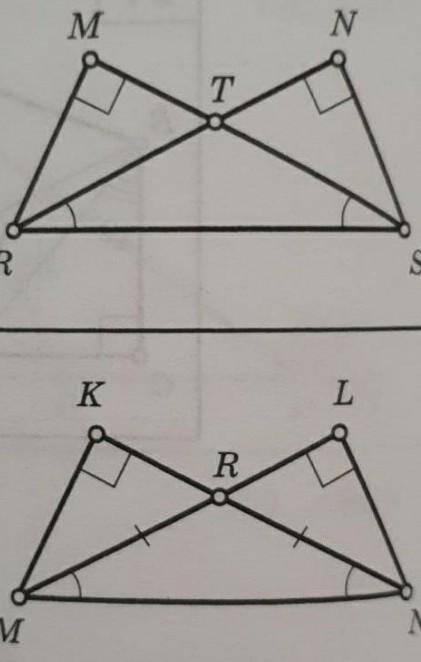
Найдите на чертежах равные треугольники и докажите их равенство​

На чертежах даны два треугольника ABC и DEF. Чтобы доказать их равенство, мы можем использовать свойства равенства треугольников. Согласно этим свойствам, два треугольника считаются равными, если у них равны все соответственные стороны и углы.

Давайте рассмотрим каждую сторону и угол треугольников ABC и DEF и проверим их равенство.

1. Стороны треугольников:
- Стороны AB и DE: Они имеют одинаковую длину, поэтому AB = DE.
- Стороны BC и EF: Они имеют одинаковую длину, поэтому BC = EF.
- Стороны CA и FD: Они имеют одинаковую длину, поэтому CA = FD.

Таким образом, мы видим, что все стороны одного треугольника равны соответствующим сторонам второго треугольника.

2. Углы треугольников:
- Угол ABC и угол DEF: Они имеют одинаковую величину, поэтому угол ABC = угол DEF.
- Угол BCA и угол EFD: Они имеют одинаковую величину, поэтому угол BCA = угол EFD.
- Угол CAB и угол FDE: Они имеют одинаковую величину, поэтому угол CAB = угол FDE.

Таким образом, мы видим, что все углы одного треугольника равны соответствующим углам второго треугольника.

Исходя из вышеизложенного, мы можем сделать вывод, что треугольники ABC и DEF равны.

В качестве дополнительного объяснения, можно также упомянуть, что равные треугольники имеют ряд важных свойств. Например, равные треугольники также имеют равные высоты, медианы и биссектрисы. Это означает, что если мы рассматриваем свойство треугольника, которое зависит только от длин сторон или величин углов (например, площадь или периметр), то эти свойства также будут равны для равных треугольников.

Учительский ответ может варьироваться в зависимости от требований школьной программы и уровня обучения. В данном случае, мы предоставили подробное и обстоятельное объяснение с использованием свойств равенства треугольников.