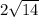Найдите катет прямоугольного треугольника, если его rипотеиуза и второй катет соответствии доpивиюють 9 см и5 см.​

Гипотинуза в квадрате равна сумме квадрата катетов. АВ²=ВС²+СD²

АВ=9; ВС=5 следовательно CD²= АВ²-ВС²

СD²=9²-5²=81-25=56

CD= корень из 56

Объяснение:

Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:

c^2 = a^2 + b^2  (^2 - вторая степень числа)

Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)

a^2 = c^2 - b^2

Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2

В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ