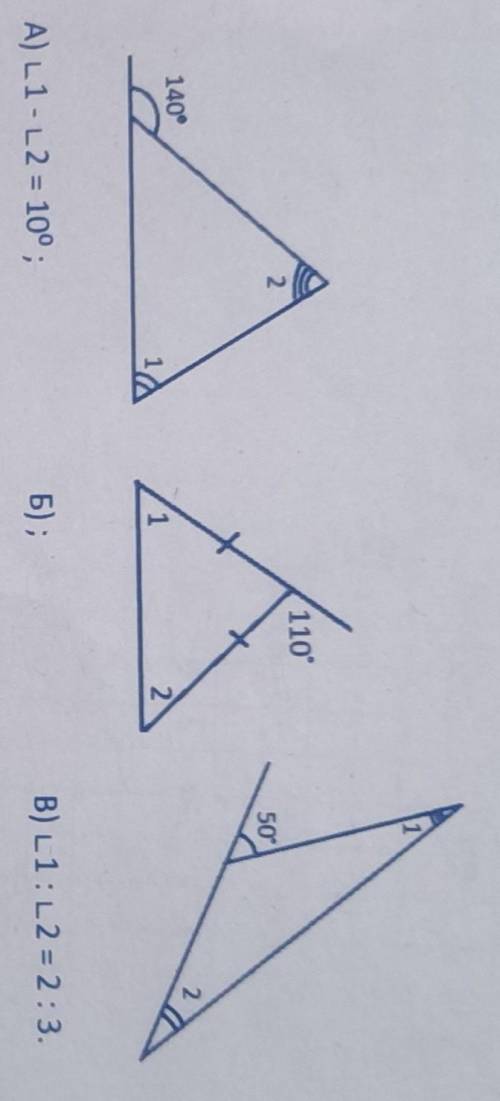
Найдите градусные меры углов 1 и 2​

а) 1=75 2=65

б) 1=2=55

в) 1=20  2=30

Объяснение:

а) 180°-140°=40°

180-40=140

140°-10°=130°

130°:2=65°=∠2

140-65=75°=∠1

б) 180-110=70

180-70=110

110÷2=55=∠1=∠2

в)

180-50=130

180-130=50

∠1+∠2=2+3=5 частей

50÷5=10=1 часть

2×10=20°=∠1

3×10=30°=∠2

Объяснение:

Решение.

АВС - треугольник.

∠1 - ∠2 =10*.

Найдем внутренний угол А.

∠А=180*-140*=40*.

На угол 1 и угол 2 остается

180*-40*=140*;

∠1+∠2=140*;

Известно, что ∠1 -∠2 =10*. Откуда ∠1=∠2+10*;

∠2+10*+∠2 = 140*;

2∠2=140*-10*;

∠2=65*;

∠1-∠2=10*;

∠1=10*+∠2=10*+65*=75*.

***

Дано треугольник АВС. Внешний угол В равен 110*.

Найдем внутренний угол В:

∠В=180*-110*=70*;

Δ АВС  - равнобедренный (по условию), у котрого углы при основании равны ∠1=∠2.

∠1=∠2=(180*-70*)/2 = 55*.

***

Дано тупоугольный треугольник АВС.

Внешний угол при вершине равен 50*.

Найдем внутренний угол В:

180*-50*=130*.

∠1+∠2=180*-130*=50*;

Пусть угол 1 равен 2х. Тогда угол 2 равен 3х.

2х+3х=50*;

5х=50*;

х=10*;

Угол 1 равен 2х=2*10=20*;

Угол 2 равен 3х=3*10=30*.