Найдите длину радиуса окружности,вписанной в правильный многоугольник, если длина его стороны равна 15 см, а длина радиуса окружности,описанной вокруг эт ого многоугольника равна 5 корней из 3 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Установіть особливості клімату регіонів України за аналізом кліматичних...
1 - Решите задачу . Чему равен периметр треугольника, если его стороны относятся...
1 - присоединения деталей когда требуется переодич замена элементов?...
2 - Написать реакции взаимодействия углекислого газа со щелочью, карбонатом...
3 - 1. Кто изображён на картине Г. Г. Чернецова? Так ли вы представляете...
3 - , ЕСЛИ НЕ ЗНАЕТЕ НЕ ОТВЕЧАЙТЕ УМОЛЯЮ >...
1 - Какой общий признак связывает причастия в следующих словосочетаниях?...
2 - A Ущелье отвесно расекало горы. Дерево вздрогнуло сагнулось и опять разпрямилось....
2 - заполнить таблицу Изменение пищи в пищеварительном тракте при участии...
1 - Если поставить кросовок 41 размера на лист в клетку и обвести сколько...
2
Радиус вписанной окружности - это высота равнобедренного треугольника, где боковые стороны - радиусы описанной окружности, а основание - сторона многоугольника
r = корень(R^2 - (a/2)^2) = корень(300 - 225) = 5*корень(3)
Из формулы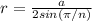 , где а - сторона многоугольника, найдем синус угла.
, где а - сторона многоугольника, найдем синус угла.
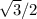 . Это значит, что n=3 - у нас правильный треугольник.
. Это значит, что n=3 - у нас правильный треугольник.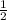 . То есть, радиус вписанной:
. То есть, радиус вписанной: 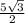
Он равен
Радиусы вписанной и описанной окружностей у правильного треугольника относятся как