1. Геометрия
  2. Найдите длину отрезка

Найдите длину отрезка ef и координаты его середины, если e(-5; 2) и f(7; -6)

Adilka11 Adilka11    1   06.10.2019 23:20    80

Ответы
MagistooorNaine MagistooorNaine  10.10.2020 00:34
ответ:

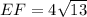EF = 4\sqrt{13} ед; O\: \: (1; \: -2)

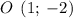
Объяснение:

1) Найдём длину отрезка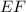 EF.

Длина отрезка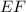 EF - это расстояние от точки 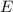E до точки F.

EF = \sqrt{{\Big(F_{(x)} - E_{(x)}\Big)}^{2} + {\Big(F_{(y)} - E_{(y)}\Big)}^2} = \sqrt{{\Big(7 - (-5)\Big)}^2 + {(-6 - 2)}^2} = 4\sqrt{13}

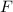2) Найдём координаты середины отрезка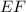 EF.

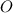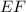Пусть точка O - середина отрезка EF.

O_{(x)} = \dfrac{\Big(E_{(x)} + F_{(x)}\Big)}{2} = \dfrac{(-5 + 7)}{2} = 1\\\\O_{(y)} = \dfrac{\Big(E_{(y)} + F_{(y)}\Big)}{2} = \dfrac{\Big(2 + (-6)\Big)}{2} = -2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Tusurgaliev11 Tusurgaliev11  20.09.2019 06:20
Площадь осевого сечения цилиндра равна 12 корней из пи дм в квадрате, площадь основания цилиндра равна 25 дм в квадрате.найти объем цилиндра?...
aziko2002 aziko2002  09.09.2021 12:52
Дано трикутник авс Кут с=90° СК перпендикулярний АВ, ВК=9 см, АК=16 см найти АС, СВ...
Marrrrrrk Marrrrrrk  09.09.2021 12:50
5. Площа паралелограма 70 см, висота дорівнює 7 см. Знайдіть довжину сторони, до якої проведено цю висоту. А) 10 см; Б) 5 см ; В) 20 см; Г) 14 см....
скмниниручвк скмниниручвк  09.09.2021 12:48
Периметр рівнобедриного трикутника дорівнює 17 см , а його основа дорівнює 5 см . Знайдіть бічну сторону трикутника ?...
nigap nigap  09.09.2021 12:45
Обчисліть кут, під яким перетинаються бісекриси AM CN трикутника ABC якщо кут A=100 градусів, кут C= 20...
michlich michlich  09.09.2021 12:42
Доказать, что угол x равен углу y...
0Jocker0 0Jocker0  09.09.2021 12:41
Периметр рівнобедриного трикутника дорівнює 10 см , а його основа дорівнює 5 см . Знайдіть бічну сторону трикутника ?...
милуя милуя  09.09.2021 12:41
Відрізок MN паралельний до сторони AC трикутника ABC. MN = 9 см, AC = 12 см, MB = 6 см. Знайдіть довжину AB. 1 А) 9 см; Б) 18 см; 3 В) 8 см; Г) 24 см....
kseniazorina14 kseniazorina14  18.05.2020 08:16
1.Составьте упавнение прямой, проходящей через точки А(7;0) и В(-3; 1). Найдите ее угловой коэффициент и точки пересечения прямой с осями координат....
Nikuiii Nikuiii  18.05.2020 08:16
Окружность центром О вписана В равнобедренную трапецию ABCD и касается с боковой стороной CD в точке K если известно CK равно 1 см CD равно 4 см Найдите площадь трапеции​...

Популярные вопросы