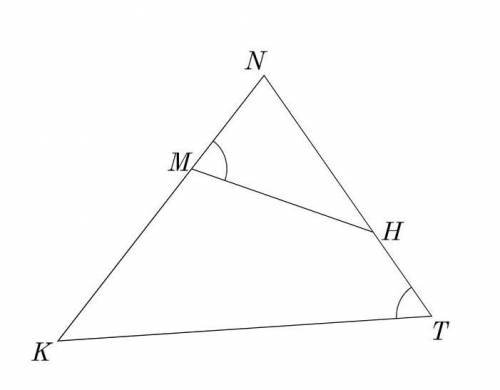
Найди значение периметра треугольника MNH, если KM = 6,8
MN = 4, NT=14,4, KT=21,6.
Ответы
Для решения этой задачи нам понадобятся знания о свойствах треугольников и формулах для нахождения периметра треугольника.
Первым шагом, мы можем найти значение длины отрезка NT, используя формулу пифагора. По формуле пифагора, сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. В данном случае, отрезок NT является гипотенузой. Для нахождения ее длины, мы можем использовать катеты KT и KN:
NT^2 = KT^2 + KN^2
14.4^2 = 21.6^2 + KN^2
207.36 = 466.56 + KN^2
KN^2 = 207.36 - 466.56
KN^2 = -259.20
Видим, что значение KN^2 получилось отрицательным. Это означает, что треугольник МНК не существует в данном случае. Отрезок КН не может быть отрицательным, так как является длиной отрезка. Используя эту информацию, мы можем сделать вывод, что задача задана некорректно и не имеет решения.
Таким образом, мы не можем найти значение периметра треугольника MNH, так как треугольник МНК не существует в данном случае.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- В отличие от мхов у хвощей имеются...
3 - Умоляю ответьте хоть кто-нибудь... Я седьмой раз за потратила...
1 - Утворіть присвійні прикметники від іменників : Тетяна, Микола,...
2 - Соотнесите термины и определения: 1) окрольничий; 2) опричнина;...
3 - План-характеристика по этим темам в фото , хотя бы одно , обязательно...
3 - До ть будь ласка! Перебудуйте речення з відокремленими зворотами...
1 - с кыргызским языком Упр 273 и 274 ...
3 - Як ПОЗНАЧАЮТЬСЯ нестійкі звуки? ДУЖЕ ЛЕГКО! Музика...
1 - Task 1. Decide on the part of speech for each of the words in bold...
2 - Назови виды животных, у которых самка является заботливой матерью(...
3