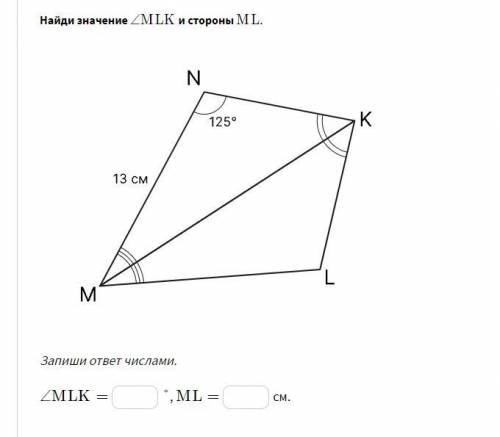
Найди значение MLK ∠MLK и стороны ML

Хорошо, давайте решим вместе эту задачу. На рисунке дан треугольник MNL, где M, N и L -- его вершины. Нам нужно найти значение угла MLK (пусть это будет угол α) и длину стороны ML. 1. Начнем с определения угла α. Мы знаем, что сумма углов треугольника равна 180 градусов. Это означает, что α + ∠NML + ∠LKM = 180°. 2. На рисунке дано, что угол ∠NML = 65°, поэтому мы можем написать уравнение: α + 65° + ∠LKM = 180°. 3. Теперь сосредоточимся на ∠LKM. Мы знаем, что угол на основании равнобедренного треугольника равен (180° - углу при вершине) / 2. 4. В данном случае, угол при вершине является углом ∠ALC. Поэтому, ∠LKM = (180° - ∠ALC) / 2. 5. Чтобы найти ∠ALC, мы можем использовать факт, что сумма углов треугольника равна 180 градусов: ∠ALC + ∠CLA + ∠LAC = 180°. 6. На рисунке дано, что ∠LAC = 22°. Поэтому, мы можем записать уравнение ∠ALC + 75° + 22° = 180°. 7. Решив это уравнение, мы найдем, что ∠ALC = 83°. 8. Подставим это значение в наше предыдущее уравнение: ∠LKM = (180° - 83°) / 2 = 97° / 2 = 48.5°. Таким образом, мы нашли, что угол MLK (α) равняется 48.5°. 9. Вычислим длину стороны ML. Поскольку у нас нет прямоугольного треугольника или других данных, мы должны использовать закон синусов. Закон синусов гласит, что соотношение между сторонами и синусами противолежащих углов в треугольнике есть постоянная величина: a / sin(A) = b / sin(B) = c / sin(C). 10. Мы знаем угол α (48.5°), сторону MN (4.5 см), и сторону NL (2 см). Обозначим сторону ML как x. Тогда, мы можем записать уравнение, используя закон синусов: x / sin(48.5°) = 2 / sin(65°). Подставляем значения, которые у нас есть, и решаем уравнение относительно x. x / 0.7536 = 2 / 0.9063 x = (2 x 0.7536) / 0.9063 x = 1.5072 / 0.9063 x ≈ 1.6611 см. Таким образом, длина стороны ML равна примерно 1.6611 см. Итак, мы нашли значение угла MLK (α), которое равно 48.5°, и длину стороны ML, которая равна примерно 1.6611 см.