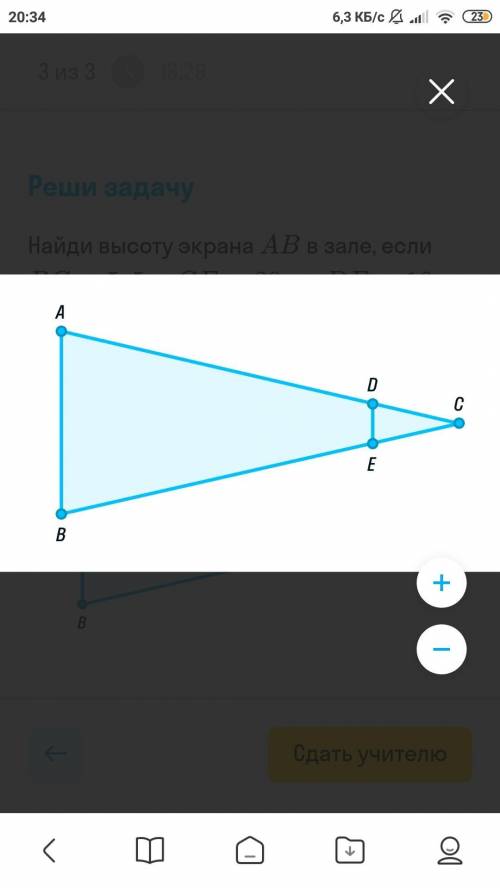
Найди высоту экрана АВ в зале, если ВС=5,5 м, СЕ=20 см, DE=16 см, DE//AB

Для решения этой задачи, нам понадобятся две пары подобных треугольников - треугольник СDE и треугольник СBA.

На основе параллельности DE и AB, мы можем установить, что отношение соответствующих сторон этих треугольников будет одинаковым. То есть:

DE/AB = CE/BC

Теперь подставим известные значения в это соотношение:

16 см / AB = 20 см / BC

Необходимо найти высоту экрана AB, поэтому нам нужно найти значение BC.

Для этого мы можем использовать треугольник БСЕ. В нем сумма углов в любом треугольнике равна 180 градусов, поэтому у нас есть:

Угол СEB + угол BEC + угол BCE = 180 градусов

Угол СEB = 90 градусов (так как угол между параллельными линиями и пересекающей их линией равен 90 градусов)

90 градусов + угол BEC + угол BCE = 180 градусов

Теперь мы знаем, что угол BEC + угол BCE = 180 - 90 = 90 градусов.

Углы BEC и BCE являются смежными и, следовательно, дополнительными (то есть, их сумма равна 180 градусов). Поэтому каждый из этих углов равен 90 / 2 = 45 градусов.

Далее, обратимся к треугольнику BСЕ.

Так как BE=EC (это можно вывести из параллельности DE и AB), у нас есть прямоугольный треугольник BЕС с углом ВЕС, равным 45 градусов.

Теперь мы можем использовать тригонометрию для нахождения значения BC. Для этого применим тангенс угла ВЕС:

тангенс угла ВЕС = BC / BE

тангенс 45 градусов = BC / 5,5 м

1 = BC / 5,5 м

BC = 5,5 м

Теперь мы можем подставить значение BC в исходное соотношение:

16 см / AB = 20 см / 5,5 м

Так как значения измерения длины должны быть в одних и тех же единицах измерения, нам нужно преобразовать 5,5 м в сантиметры:

5,5 м = 5,5 * 100 см = 550 см

16 см / AB = 20 см / 550 см

Чтобы найти значение AB, выразим его через пропорцию:

16 см * 550 см = 20 см * AB

8800 см^2 = 20 см * AB

AB = 8800 см^2 / 20 см

AB = 440 см

Таким образом, высота экрана AB в зале равна 440 см или 4,4 метра.