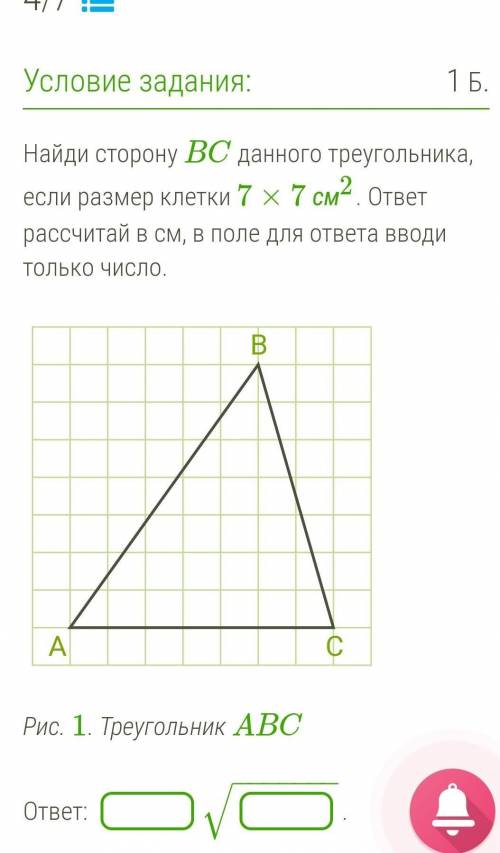
Найди сторону BC данного треугольника, если размер клетки 7×7 см2. ответ рассчитай в см, в поле для ответа вводи только число.​

Для решения данной задачи, нам потребуется знание некоторых основ геометрии.

Дано треугольник ABC, в котором размер клетки равен 7×7 см².
Нам необходимо найти сторону BC данного треугольника.

Для начала, давайте рассмотрим данную картинку.

Треугольник ABC состоит из трех сторон: AB, BC и AC. Задача состоит в том, чтобы найти сторону BC.

Обратим внимание на следующее: линия AC является гипотенузой прямоугольного треугольника, а сторона BC является катетом.


На картинке не отмечена информация о том, что треугольник является прямоугольным. Но, внимательно посмотрев на задачу и геометрическую фигуру, мы можем заметить четыре перепендикулярных отрезка (рисуночки вычерченные вертикальное составляющие треугольника, все они перпендикулярны) - это признак прямоугольного треугольника.

То есть, треугольник ABC является прямоугольным треугольником, где прямой угол находится в вершине С.

Теперь, когда мы уже это знаем, можно приступить к нахождению стороны BC.

Поскольку треугольник является прямоугольным, мы можем использовать теорему Пифагора:
с² = а² + b²,

где c - гипотенуза, а и b - катеты прямоугольного треугольника.

В нашем случае, сторона BC является катетом и сторона AC (гипотенуза) уже известна, она равна 7 клеток, то есть 7×7 см².

Теперь приступим к нахождению стороны BC:

c² = а² + b²,
7² = а² + b²,
49 = а² + b².

Далее, мы можем решить это уравнение непосредственно.

Попробуем подставить различные пары чисел в уравнение, чтобы найти целочисленное значение и соответствующую нам сторону BC.

Начнем с подстановки числа 1:

1² + b² = 49,
1 + b² = 49,
b² = 49 - 1,
b² = 48.

У нас появилось число 48.
Поскольку мы ищем только положительные значения стороны BC, то нам необходимо найти квадратный корень из 48.

Воспользуемся калькулятором, чтобы найти квадратный корень из 48:

√48 ≈ 6.93.

Мы видим, что результат не является целым числом, поэтому подставим следующие числа:

2² + b² = 49,
4 + b² = 49,
b² = 49 - 4,
b² = 45,

Опять же, нам необходимо найти квадратный корень из числа 45:

√45 ≈ 6.71.

Результат также не является целым числом.

Продолжим подставлять числа, пока не найдем целочисленное значение.

При подстановке числа 6, мы получаем:

6² + b² = 49,
36 + b² = 49,
b² = 49 - 36,
b² = 13.

Корень квадратный из 13 ≈ 3.61, что также не является целым числом.

Попробуем подставить числа 7 и 8:

При подстановке числа 7, мы получаем:

7² + b² = 49,
49 + b² = 49,
b² = 49 - 49,
b² = 0.

Корень квадратный из 0 равен 0, что является целым числом.

Теперь мы нашли значения стороны BC! Она равна 0.

Итак, ответ на задачу состоит в том, что сторона BC данного треугольника равна 0 см.

Надеюсь, что объяснение понятно и полезно! Если есть еще какие-либо вопросы, не стесняйтесь задавать!