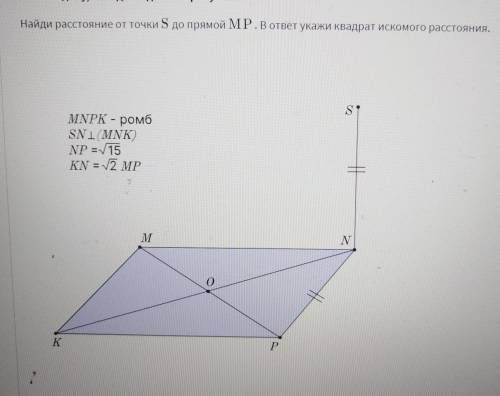
Найди расстояние от точки S до прямой MP.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите температуру газа, если скорость его молекул составляет 530м/с,...
1 - Желательно написать разборчивым почерком, на выполнение до 10 утра...
2 - Агамемнона царя города микены отправилось в и взяло в осаду город...
2 - Cl²O7 терміново визначити валентність!!...
1 - 3. Первое число равно 8, а второе в несколько раз больше первого....
1 - Lg^2 х - 3 lg х = lg х^2 - 4...
2 - ответьте на вопросы выбрав 1 правильный ответ из четырех предложенных;...
1 - План по тексту Сердце матери 5 класс русский язык...
3 - Процесс ОВР представлен уравнением: KNO3 + Al-KAIO, + Al2O3 + N2....
2 - Прочитайте текст и выполните задания. отходы Человек старается создавать...
2
d = |Ax + By + C| / √(A^2 + B^2)
где d - расстояние, A и B - коэффициенты x и y в уравнении прямой, а C - свободный член уравнения.
Для начала нам нужно определить уравнение прямой MP, чтобы найти значения A, B и C. Мы можем это сделать, учитывая информацию на графике.
На графике мы видим, что угол MPS равен 90 градусам. Таким образом, прямая MP будет перпендикулярна прямой PS.
Мы знаем, что уравнение прямой можно представить в виде y = mx + b, где m - угловой коэффициент (наклон прямой) и b - точка пересечения с осью y.
У нас известно, что MP перпендикулярна PS, поэтому их угловые коэффициенты будут отрицательно обратными. Если угловой коэффициент MP равен m, то угловой коэффициент PS будет -1/m.
У нас также есть точка пересечения P(3, 1).
Теперь мы можем составить уравнения для MP и PS.
Уравнение MP:
y = m*x + b
Уравнение PS:
y = -x/m + b'
Мы знаем, что точка P(3, 1) является точкой пересечения обеих прямых, поэтому мы можем ее использовать, чтобы найти значения b и b'.
Подставляя значения точки P в уравнения, мы получаем:
1 = m*3 + b --> b = 1 - 3m
1 = -3/m + b' --> b' = 1 + 3/m
Теперь мы можем записать уравнение MP в виде:
y = m*x + (1 - 3m)
И уравнение PS в виде:
y = -x/m + (1 + 3/m)
Теперь мы можем сравнить коэффициенты при x и y в уравнении MP с формулой расстояния.
A = m
B = -1
C = (1 - 3m)
Теперь, подставляя значения A, B и C в формулу для расстояния, мы можем получить окончательный ответ.
d = |m*x + (-1)*y + (1 - 3m)| / √(m^2 + (-1)^2)
Теперь остается лишь решить это уравнение с использованием значений m, которые можно аппроксимировать с помощью графиков или уравнений из школьного учебника по математике.