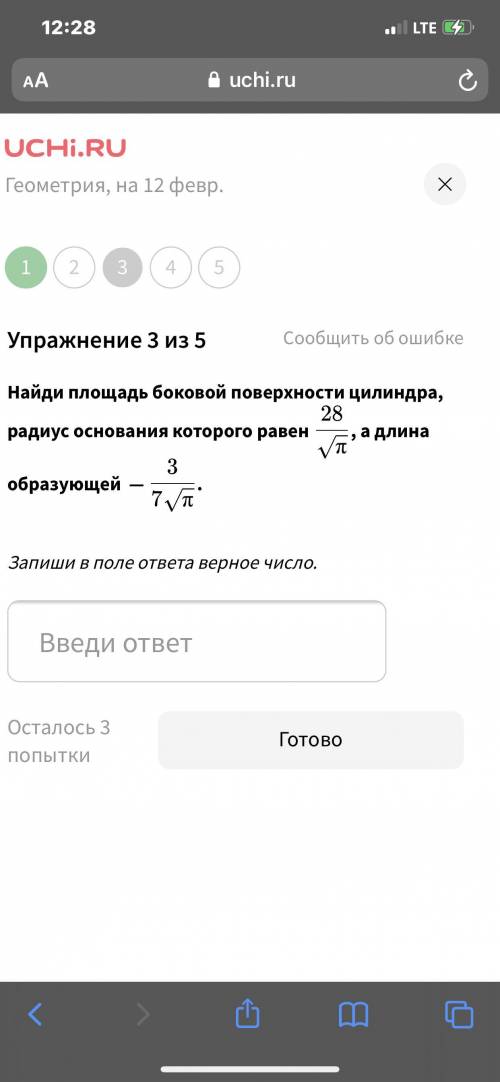
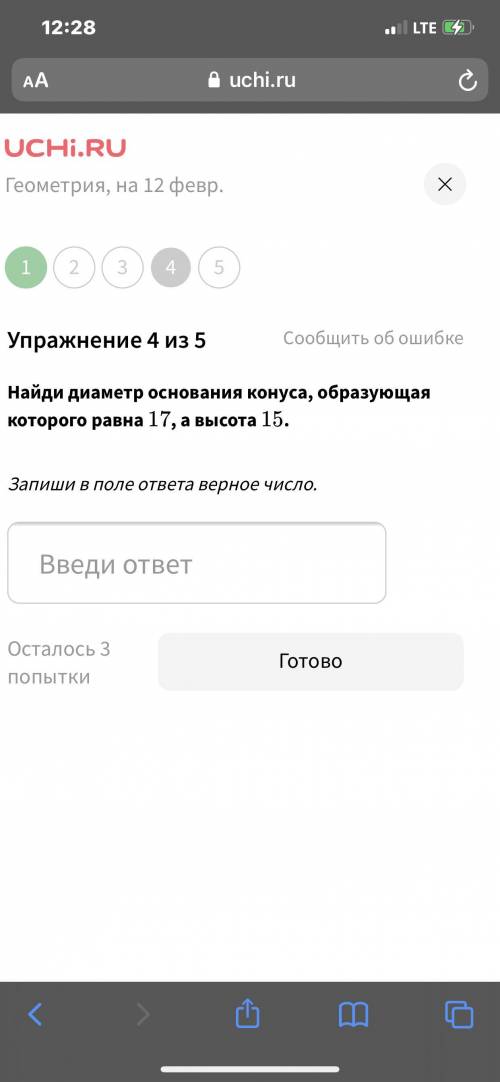
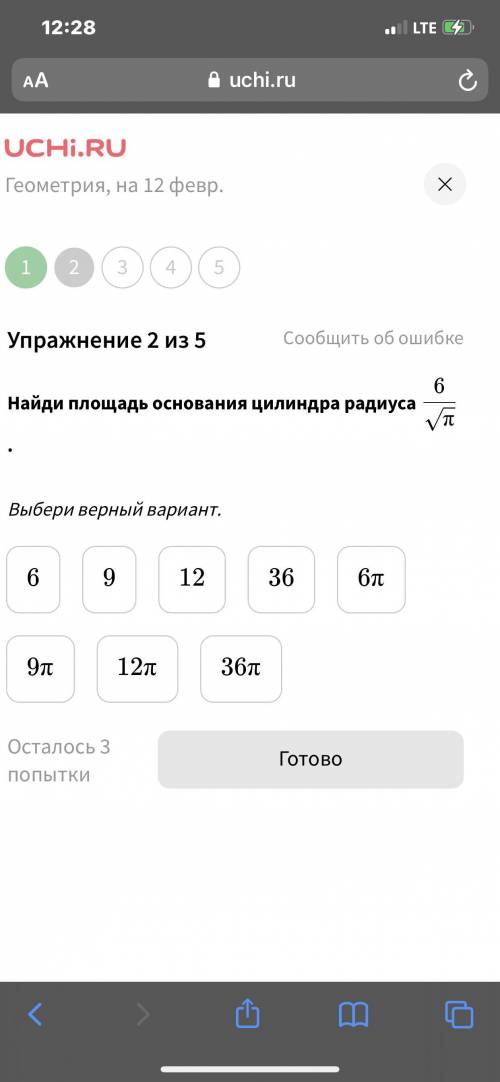
Найди площадь основания цилиндра радиуса 6/ корень п решить задания на фото

Для начала рассмотрим, что представляет собой площадь основания цилиндра. Основание цилиндра - это кругляш, которым цилиндр опирается на поверхность. В данной задаче нам нужно найти площадь этого круга. Площадь круга можно найти по формуле: S = π * r², где S - площадь круга, а r - радиус круга. В данной задаче дан радиус цилиндра - 6/корень п. Чтобы решить эту задачу, нам нужно найти значение радиуса. На фото дана формула объема цилиндра: V = S * h, где V - объем цилиндра, S - площадь основания цилиндра, h - высота цилиндра. Также на фото дано значение объема цилиндра - 36/корень п. Мы также можем заметить, что высота цилиндра равна 3 (это значение не дано на фото, но мы можем судить об этом по остальным данным и изображению). Теперь мы можем найти площадь основания цилиндра, используя ранее введенную формулу для площади круга и значения радиуса. Подставим значения в формулу: S = π * (6/корень п)². Распишем выражение и выполним некоторые математические действия: S = π * (6/корень п)² S = π * (36/п) S = 36π/п. Таким образом, площадь основания цилиндра радиуса 6/корень п равна 36π/п.