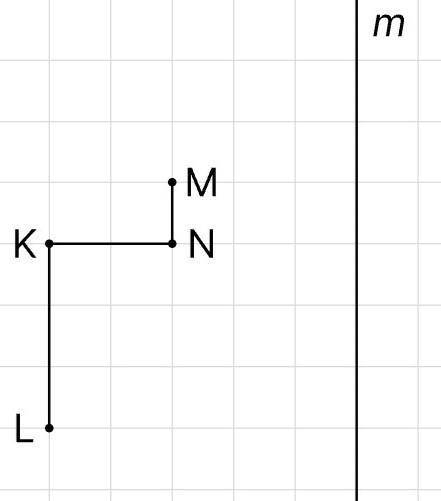
Найди площадь многоугольника, который получится при осевой симметрии ломаной MNKL относительно прямой m. Размер одной клетки равен 1. Запиши ответ числом:

Симметрия значит, что фигура справа и слева одинаковы. Посчитаем количество клеток слева -18. Справа столько же - ответ 36.

Для нахождения площади многоугольника, который получится при осевой симметрии ломаной MNKL относительно прямой m, нужно сначала найти симметричные точки относительно прямой m для всех вершин ломаной. Затем соединить найденные симметричные точки прямыми линиями, чтобы получить симметричный многоугольник. Далее нужно посчитать площадь этого многоугольника.

Итак, давайте найдем симметричные точки для каждой вершины ломаной MNKL относительно прямой m.

1. Начнем с вершины M. Поскольку прямая m является осью симметрии, симметричной точкой будет вершина M сама по себе. Обозначим эту точку как M1.

2. Перейдем к вершине N. Чтобы найти симметричную точку для N, мы проводим перпендикуляр к прямой m из N и продлеваем его на такое же расстояние от прямой m. Пересечение этого перпендикуляра с прямой m даст симметричную точку для N. Обозначим эту точку как N1.

3. Таким же образом находим симметричные точки для K и L. Обозначим их как K1 и L1 соответственно.

Теперь у нас есть симметричные точки M1, N1, K1 и L1. Чтобы получить симметричный многоугольник, соединим эти точки прямыми линиями, как показано на рисунке.



Теперь рассмотрим полученный многоугольник. Он состоит из двух прямоугольников и одного треугольника.

1. Рассмотрим первый прямоугольник, который образован вершинами M, N1, M1 и N. Чтобы найти площадь этого прямоугольника, нужно вычислить его длину и ширину. Длина прямоугольника равна расстоянию между точками M и N, а ширина - расстояние между точками N и N1. Поскольку размер одной клетки равен 1, мы можем определить длину прямоугольника как 5 клеток и ширину как 2 клетки. Тогда площадь первого прямоугольника равна 5 * 2 = 10 квадратных клеток.

2. Рассмотрим второй прямоугольник, который образован вершинами N1, K, N и K1. Аналогичным образом, расстояния между этими точками равны 3 клеткам и 3 клеткам. Следовательно, площадь второго прямоугольника также равна 3 * 3 = 9 квадратных клеток.

3. Наконец, рассмотрим треугольник, который образован вершинами K1, L1 и K. Чтобы найти площадь этого треугольника, нужно вычислить его высоту и основание. Высота треугольника равна расстоянию между точкой K и отрезком L1K1, а основание - длине отрезка K1L1. Определить расстояние и длину отрезка можно, используя размеры клеток. В данном случае, расстояние равно 2 клеткам, а длина - 1 клетка. Следовательно, площадь треугольника равна (1 * 2) / 2 = 1 квадратная клетка.

Теперь, чтобы найти полную площадь многоугольника, нужно сложить площади всех трех фигур:

10 квадратных клеток + 9 квадратных клеток + 1 квадратная клетка = 20 квадратных клеток.

Таким образом, площадь многоугольника, который получится при осевой симметрии ломаной MNKL относительно прямой m, равна 20. Ответ записывается числом.