Найди периметр треугольника ABC, если его вершины имеют следующие координаты: A(1;2), B(6;11) и C(8;9).

Ответы

NiceLeave 14.09.2020 12:23

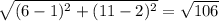
AB = $\sqrt{(6-1)^{2} + (11-2)^{2} } = \sqrt{106}$

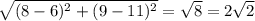
BC = $\sqrt{(8-6)^{2} + (9-11)^{2} } = \sqrt{8} = 2\sqrt{2}$

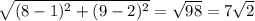
AC = $\sqrt{(8-1)^{2} + (9-2)^{2} } = \sqrt{98} = 7\sqrt{2}$

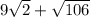
P = $9\sqrt{2} + \sqrt{106}$

ПОКАЗАТЬ ОТВЕТЫ

cazuncko2016 27.01.2024 22:48

Чтобы найти периметр треугольника ABC, нам нужно измерить длины его сторон и сложить их.

Сначала найдем длину стороны AB. Для этого используем формулу расстояния между двумя точками в декартовой системе координат:

AB = √((x2 - x1)² + (y2 - y1)²)

Где (x1, y1) - координаты точки A, а (x2, y2) - координаты точки B.

Подставим значения координат:

AB = √((6 - 1)² + (11 - 2)²)
= √(5² + 9²)
= √(25 + 81)
= √106

AB ≈ 10.29

Теперь найдем длину стороны BC, используя аналогичную формулу:

BC = √((x2 - x1)² + (y2 - y1)²)

Где (x1, y1) - координаты точки B, а (x2, y2) - координаты точки C.

Подставим значения координат:

BC = √((8 - 6)² + (9 - 11)²)
= √(2² + (-2)²)
= √(4 + 4)
= √8

BC ≈ 2.83

Наконец, найдем длину стороны CA:

CA = √((x2 - x1)² + (y2 - y1)²)

Где (x1, y1) - координаты точки C, а (x2, y2) - координаты точки A.

Подставим значения координат:

CA = √((1 - 8)² + (2 - 9)²)
= √((-7)² + (-7)²)
= √(49 + 49)
= √98

CA ≈ 9.90

Теперь сложим длины всех сторон, чтобы получить периметр треугольника ABC:

Периметр = AB + BC + CA
≈ 10.29 + 2.83 + 9.90
≈ 23.02

Таким образом, периметр треугольника ABC составляет примерно 23.02 условных единиц длины.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия