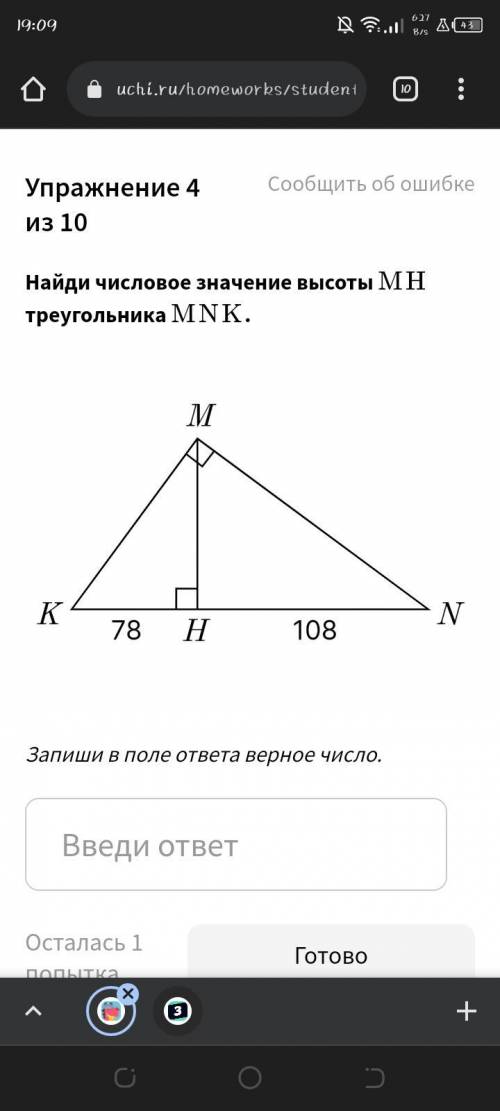
Найди числовое значение высоты MH треугольника MNK

Добрый день! Давайте решим вместе задачу. Мы должны найти числовое значение высоты MH треугольника MNK. Для этого нам понадобятся некоторые свойства треугольников. Свойство 1: В треугольнике высота, проведенная к основанию, делит его на два прямоугольных треугольника. Свойство 2: В прямоугольном треугольнике катет и гипотенуза связаны между собой с помощью теоремы Пифагора. Итак, давайте по порядку. В задаче дан треугольник MNK, и мы ищем высоту MH. Основание треугольника - это сторона MN. В задаче дано значение основания, MN = 8 см. Для начала, нам понадобится найти площадь треугольника MNK. 1. Найдем площадь треугольника MNK. Площадь треугольника можно найти по формуле S = (1/2) * a * h, где S - площадь, a - основание и h - высота. В нашем случае, a = MN = 8 см. Мы не знаем высоту h, поэтому обозначим ее как x. Таким образом, S = (1/2) * 8 * x = 4x. 2. Посчитаем площадь треугольника MNK другим способом. Так как в треугольнике всегда есть площадь, мы можем найти ее, зная длины всех сторон треугольника. Для этого применим формулу Герона. Даны стороны треугольника MNK: MK = 10 см, NK = 6 см и MN = 8 см. По формуле Герона, площадь треугольника выражается следующим образом: S = √(p*(p - a)*(p - b)*(p - c)), где p - полупериметр треугольника, a, b, c - длины сторон треугольника. Полупериметр треугольника вычисляется по формуле p = (a + b + c) / 2. В нашем случае, a = 8 см, b = 10 см и c = 6 см. Подставляя значения в формулу, получаем: p = (8 + 10 + 6) / 2 = 24 / 2 = 12 см S = √(12*(12 - 8)*(12 - 10)*(12 - 6)) = √(12*4*2*6) = √(576) = 24 см². 3. Запишем равенство обеих найденных площадей и найдем высоту. 4x = 24 x = 24 / 4 x = 6 см Таким образом, высота треугольника MH равна 6 см. Мы использовали свойства треугольников и формулы для нахождения площади треугольника. Надеюсь, объяснение было понятным и полезным для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать их. Желаю успехов в обучении!