Напиши уравнение окружности, которая проходит через точку 10 на оси Ox и через точку 3 на оси Oy, если известно, что центр находится на оси Ox. (Дроби максимально сократите. Если в ответе получилось целое число, то запишите его в виде дроби со знаменателем 1.)
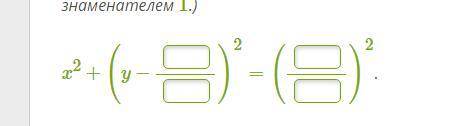
Ответы
Для решения этой задачи мы можем использовать стандартную формулу уравнения окружности, которая имеет вид (x - a)^2 + (y - b)^2 = r^2, где (a, b) - координаты центра окружности, r - радиус окружности.
Из условия задачи известно, что центр окружности находится на оси Ox. Давайте предположим, что координаты центра окружности равны (x, 0), где x - некоторая неизвестная величина.
Также известно, что окружность проходит через точку (10, 0) на оси Ox и точку (0, 3) на оси Oy. Подставляя координаты этих точек в уравнение окружности, мы получим два уравнения:
(10 - x)^2 + (0 - 0)^2 = r^2 (уравнение, соответствующее точке (10, 0) на оси Ox)
(0 - x)^2 + (3 - 0)^2 = r^2 (уравнение, соответствующее точке (0, 3) на оси Oy)
Упрощая эти уравнения, получаем:
(10 - x)^2 = r^2
x^2 + 9 = r^2
Теперь мы получили систему из двух уравнений:
(10 - x)^2 = r^2
x^2 + 9 = r^2
Приравняем выражения для r^2:
(10 - x)^2 = x^2 + 9
Раскрывая скобки:
100 - 20x + x^2 = x^2 + 9
Упрощая уравнение:
20x = 91
Теперь найдем значение x:
x = 91/20
Теперь, зная x, мы можем вычислить r^2, подставив значение x в одно из исходных уравнений:
x^2 + 9 = r^2
(91/20)^2 + 9 = r^2
8281/400 + 9 = r^2
8841/400 = r^2
Таким образом, уравнение окружности, которая проходит через точку (10, 0) на оси Ox и точку (0, 3) на оси Oy, при условии что ее центр находится на оси Ox, будет иметь вид:
(x - 91/20)^2 + y^2 = 8841/400
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Дано m=500кг,h=10м,t=25c,ккд=70%,U=380В,знайти І ?...
2 - Параллельно оси цилиндра на растоянии 16 см от неё, проведено сечение....
3 - Влияние татаро-монгольского нашествия на Русь Примерный план выступления...
1 - БЫСТРЕ 6. Продовжте речення й укажіть назви творів, у яких діють...
1 - 3. У выражение:4a2-12ав+в22a- Звдроби при а=2 и в=3...
3 - Определите сколько граммов соли содержится в 3 литрах воды Балтийского...
1 - Сочинение рассуждение почему нужно беречь природу...
2 - 8. В каком ряду во всех словах следует писать букву И ? А) спец..алист,...
1 - Тема: Алкины. Физические и химические свойства. Видео-урок:https://youtu.be/YW-ax0abkvk...
3 - 217Bagara,Hopina za 1 gert hou to greu how to manne(со инаковая36Pemerue202800П(ка...
3