Написать уравнение плоскости, проходящей через начало координат, перпендикулярной прямой (x-3)/4 = (y-2)/-1 = (z+1)/1
Другие вопросы по теме Геометрия
Популярные вопросы
- 6. Төмендегі заттардың әр адамның жеке гигиенасында алатын орны...
3 - В треугольнике АВС стороны АВ 8 см ВС 15см АС 17см найдите стороны...
2 - 5.Императорға арнап неше сарай салдырды...
3 - Піднесіть до квадрата двочлени (-х+у)²; (-х-у)²; (-2х+5)²; (-2m-12n)²;...
2 - Скласти таблицю на дві цивілізації.Шумер та Китай. Природні...
2 - Есе на тему порівняти образи ангелів у малковича і кирпи.(обсяг...
2 - Составь из этих слов предложения и сделай их перевод – 1. mystery-...
3 - У циліндрі проведено переріз площиною, паралельною до осі циліндра....
3 - До неістот належить слово клас(шкільний)?...
2 - На стороні ВС кута АВС позначили точку К і через неї провели...
1
Здесь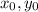 и
и 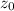 ‑ координаты точки M, лежащей на плоскости P, A, B и C ‑ координаты вектора, перпендикулярного плоскости P. Этот вектор называется нормальным к плоскости P. он же является и направляющим вектором заданной прямой.
‑ координаты точки M, лежащей на плоскости P, A, B и C ‑ координаты вектора, перпендикулярного плоскости P. Этот вектор называется нормальным к плоскости P. он же является и направляющим вектором заданной прямой.
Координаты начала координат - это нули, а направляющий вектор заданной прямой - это числа в знаменателях уравнения прямой: (4;-1;1).
Получаем уравнение искомой плоскости: