Геометрия: Надо найти мк очень с доказательствами

Надо найти мк очень с доказательствами

Ответы

Tricjt 26.09.2021 17:30

Угол KPN равен 30 градусов => напротив него сторона в 2 раза меньше гипотенузы => PN=10

По теореме пифагора PK^2=10^2-5^2=75

PK= корень 75

MK Равна 2корня75 т.к на против угла в 30градусов сторона в 2 раза меньше гипотенузы

ПОКАЗАТЬ ОТВЕТЫ

Ekaterina2558 26.09.2021 17:30

Рассмотрим треугольник NPK.

Угол PKN = 90°, по условию задачи, значит треугольник NPK — прямоугольный. Угол PKN = 90°, угол KNP = 60°. Сумма углов треугольника равна 180°, значит угол NPK = 180° – 90° – 60° = 30°. Одно из свойств прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, KN = NP : 2. NP = 2 × KN = 2 × 5 см = 10 см. Воспользуемся теоремой Пифагора (квадрат гипотенузы равен сумме квадратов катетов) и найдем второй катет.

${(NP)}^{2} = {(PK)}^{2} + {(KN)}^{2}$

${(PK)}^{2} = {(NP)}^{2} - {(KN)}^{2}$

$PK= \sqrt{{(NP)}^{2} - {(KN)}^{2}} = \sqrt{ {10}^{2} - {5}^{2} } = \sqrt{100 - 25} = \sqrt{75}$ см

Рассмотрим треугольник MPK. Идём по тому же пути.

Угол PKM = 90°, по условию задачи, значит треугольник MPK — тоже прямоугольный. Пользуемся тем же свойством прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. PK = MP : 2. MP = 2 × PK =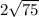 $2\sqrt{75}$ см. Применяем теорему Пифагора и находим катет KM.

${(MP)}^{2} = {(PK)}^{2} + {(KM)}^{2}$

${(KM)}^{2} = {(MP)}^{2} - {(PK)}^{2}$

$KM = \sqrt{ {(MP)}^{2} - {(PK)}^{2}} = \sqrt{ {(2 \sqrt{75} )}^{2} - {( \sqrt{75} )}^{2} } = \sqrt{4 \times 75 - 75} = \sqrt{300 - 75} = \sqrt{225} = 15$ см