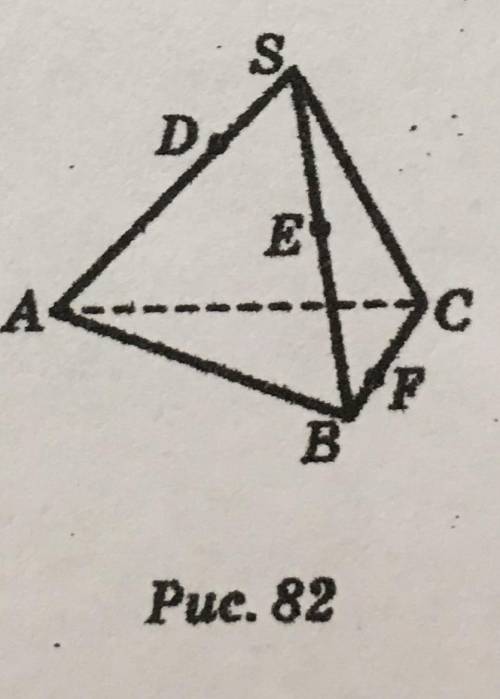
на утро нужно а то я запуталась Постройте перерез тетраэдра SABC (рис.82 прикрепила снизу ) плоскостью что проходит через точки D,E,F что принадлежат рёбрам SA,SB, и BC соотвественно

Для построения пересечения тетраэдра SABC с плоскостью, проходящей через точки D, E и F, мы можем использовать следующий алгоритм:

Шаг 1: Найдите координаты точек D, E и F
Из рисунка видно, что точка D принадлежит ребру SA, точка E принадлежит ребру SB, а точка F принадлежит ребру BC.
Таким образом, для начала нам нужно найти координаты этих точек (D, E и F). На рисунке точки A, B, C имеют заданные координаты, которые мы можем использовать для нахождения координат точек D, E и F.

Шаг 2: Постройте векторы AD, BE и CF
После нахождения координат точек D, E и F, мы можем построить векторы AD, BE и CF. Для этого вычислим разности координат между соответствующими точками. Например, вектор AD будет определяться как AD = D - A, где D и A - координаты соответствующих точек.

Шаг 3: Постройте векторное произведение BE и CF
Далее, мы строим векторное произведение между векторами BE и CF. Векторное произведение векторов дает нам нормальную векторную плоскость, проходящую через точки E и F.

Шаг 4: Постройте плоскость ABC
Для построения плоскости ABC нам необходимо найти ее нормальный вектор. Для этого мы можем использовать векторное произведение двух векторов, принадлежащих плоскости. В данном случае мы можем использовать векторы AB и AC, так как они лежат на плоскости ABC.

Шаг 5: Найти точку пересечения плоскости ABC с плоскостью DEF
Наша итоговая плоскость должна пересекать плоскость, проходящую через точки D, E и F. Для этого мы можем найти точку пересечения плоскости ABC с плоскостью DEF. Можно использовать, например, метод пересечения прямой и плоскости.

Таким образом, после выполнения всех шагов вы описанного алгоритма, мы получим пересечение тетраэдра SABC с плоскостью, проходящей через точки D, E и F.