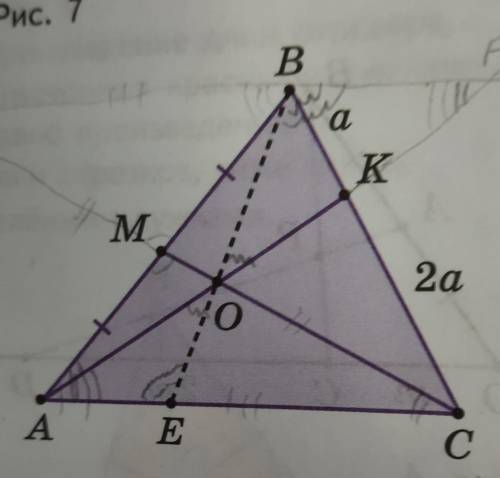
На стороне BC треугольника АВС взяли точку К так, что ВК : СК= 1 : 2. Медиана СМ пересекает отрезок АК в точке O. Прямая ВО пересекает сторону AC в точке Е. Найдите ВО : OE (рис. 8).

значит ришено

Объяснение:

Для того чтобы решить эту задачу, мы будем использовать различные свойства треугольников и отношений между их сторонами.

Давайте разберемся пошагово:

1. Заметим, что у нас есть отношение между отрезками ВК и СК - 1 : 2. Это означает, что ВК вдвое меньше СК. Можно записать это отношение как ВК = 1/2 * СК.

2. Также у нас есть информация о том, что медиана СМ пересекает отрезок АК в точке О. Отсюда можно сделать вывод, что отрезок АО также делит медиану СМ в отношении 1 : 1. Это означает, что АО равно половине длины СМ. Можно записать это как АО = 1/2 * СМ.

3. Теперь нам нужно найти отношение между отрезками ВО и ОЕ. Для этого мы изначально должны найти значения ВО и ОЕ.

4. Применим свойство подобных треугольников. Мы видим, что треугольник ВКЕ подобен треугольнику ВАС. Почему? Потому что у этих треугольников соответствующие углы равны (ВКЕ - это вертикальный угол, и угол ВАС - это угол медианы СМ, который равен 180 градусов). Кроме того, мы знаем, что отношение сторон треугольников ВКЕ и ВАС равно 1 : 2, так как ВК : СК = 1 : 2.

5. Используя свойство подобных треугольников, мы можем сказать, что ВО : ОЕ = ВК : АС. Найдем значения ВК и АС.

6. Из пункта 1 мы знаем, что ВК = 1/2 * СК. А СК - это сумма сторон СК и АК. В свою очередь, АК - это сумма сторон АО и ОК. То есть получаем: ВК = 1/2 * (СК + АК) = 1/2 * (СК + (АО + ОК)).

7. Мы также знаем, что медиана СМ делит сторону АК в отношении 1 : 1, то есть АК = 2 * АО.

8. Подставим в формулу для ВК значение АК: ВК = 1/2 * (СК + (2 * АО + ОК)).

9. Теперь посмотрим на треугольник АСМ. У него медиана СМ делит сторону АС в отношении 2 : 1. Соответственно, сторона АС равна 3 * СМ.

10. Подставим в формулу для ВК значение АС: ВК = 1/2 * (СК + (2 * АО + ОК)) = 1/2 * (СК + (2 * (1/2 * СМ) + ОК)) = 1/2 * (СК + СМ + ОК).

11. Теперь мы знаем, что ВК : АС = 1 : 2. Подставим значения ВК и АС и найдем СМ: (1/2 * (СК + СМ + ОК)) : (3 * СМ) = 1 : 2.

12. Решим это уравнение: 2 * (1/2 * (СК + СМ + ОК)) = 3 * СМ. Упростим его: СК + СМ + ОК = 3 * СМ. Получаем: СК + ОК = 2 * СМ.

13. Рассмотрим треугольник ВОЕ. Из уравнения выше мы знаем, что СК + ОК = 2 * СМ. А также заметим, что ВО = ВК - ОК. Подставим значения ВК и ОК и получим: ВО = 1/2 * (СК + СМ + ОК) - ОК = 1/2 * (СК + СМ + ОК) - 1/2 * (СК + ОК) = 1/2 * (СК + СМ + ОК - СК - ОК) = 1/2 * СМ.

14. Теперь мы знаем, что ВО = 1/2 * СМ и ОЕ = 1/2 * АС. Подставим эти значения в отношение ВО : ОЕ: 1/2 * СМ : 1/2 * АС = СМ : АС.

15. Но мы знаем, что СМ = 1/3 * АС (исходя из свойства медианы СМ в треугольнике АСМ). Подставим значение СМ и получим: СМ : АС = 1/3 * АС : АС = 1/3.

Таким образом, ВО : OE = СМ : АС = 1/3. Ответ: ВО : OE = 1 : 3.