1. Геометрия
  2. На стороне ab треугольника

На стороне ab треугольника abc отметили точку m так что угол acm=углу abc am=9 bm=7. найдите сторону ac.

Niger0000rt Niger0000rt    1   15.07.2019 20:00    5

Ответы
GINVIC GINVIC  03.10.2020 05:02
ответ:

AC = 12.

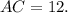
Объяснение:

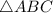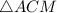Рассмотрим \triangle ABC и \triangle ACM:

\angle A - общий.

\angle ABC = \angle ACM, по условию.

\Rightarrow \triangle ABC \sim \triangle ACM, по 1 признаку подобия треугольников.

============================================================

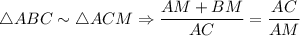
Так как \triangle ABC \sim \triangle ACM \Rightarrow \dfrac{AM + BM}{AC} = \dfrac{AC}{AM}

Пусть x - AC.

\dfrac{9 + 7}{x} = \dfrac{x}{9}

\dfrac{16}{x} = \dfrac{x}{9}

x ^{2} = \dfrac{16 \cdot 9}{1}

x^{2} =144

x = 12

12 - AC.

===========================================================


На стороне ab треугольника abc отметили точку m так что угол acm=углу abc am=9 bm=7. найдите сторону
ПОКАЗАТЬ ОТВЕТЫ
link21 link21  03.10.2020 05:02

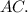
Условие: На стороне AB треугольника ABC отметили точку M так, что ∠ACM = ∠ABC, AM = 9, BM = 7. Найдите сторону AC.

Дано: ΔАВС, М ∈ АВ, ∠ACM = ∠ABC, AM = 9, BM = 7.

Найти: АС.

ΔАСМ подобен ΔАВС по двум углам:

∠ACM = ∠ABC - по условию∠А - общий угол

Составим отношения сходственных сторон:

\dfrac{AM}{AC}=\dfrac{AC}{AB}=\dfrac{CM}{CB}

\dfrac{AM}{AC}=\dfrac{AC}{AB}\;\;\;\;\Rightarrow\;\;\;\;\boldsymbol{AC^2=AM\cdot AB}

Значит,

AC=\sqrt{\big{AM\cdot AB}}=\sqrt{9\cdot 16}=\sqrt{144}=12

ответ: 12.


На стороне ab треугольника abc отметили точку m так что угол acm=углу abc am=9 bm=7. найдите сторону
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
ffjrppyegxvhd ffjrppyegxvhd  19.10.2020 09:38
3. Точка К не лежить на прямій МС. Точка А – середина відрізка КМ, точка С – середина відрізка РМ. Як розміщені прямі АР і КМ? А) перетинаються Б) мають рівно дві спільних...
WWW2023 WWW2023  19.10.2020 09:38
Контрольна робота № 2 з геометрії 7 клас Тема. Суміжні та вертикальні кутиВарiант 21. Знайдіть градусну міру кута, якщо суміжний з ним кут дорівнює 115.2. Знайдіть невідомий...
2285811 2285811  19.10.2020 09:30
Заполни таблицу, определив вид угла, смежного с данным.​...
swaTor swaTor  19.10.2020 09:38
ЕҮОБ(24,40)РЕҮОБ(24,42)​ОЙ МАТЕМ...
djhvh235 djhvh235  19.10.2020 09:39
Знайти сторону ромба,якщо його гостий кут дорівнює 60 градусів,а менша діагональ-10см....
Masha45322 Masha45322  19.10.2020 09:30
Найти смежные углы, если их градусные меры относятся как 12:6.​...
mariialebedeva mariialebedeva  25.03.2019 06:30
Через вершину с прямого угла прямоугольного треугольника авс проведена прямая сd , перпендикулярная к плоскости этого треугольника . найдите площадь треугольника abd ,...
auaftsuaftsa auaftsuaftsa  25.03.2019 06:30
Найдите радиус окружности, вписанной в прямоугольный треугольник, если его катеты равны 5 см и 12 см....
Dashocheg43 Dashocheg43  25.03.2019 06:30
Дана равнобедренная трапеция abcd,боковая сторона равно 13 см,bc равна 10 см,ad 20 см.найти площадь трапеции....
elichev3 elichev3  11.05.2020 11:37
Две прямые касаются окружности с центром О в точках М и К и пересекаются в точке Р. Найдите угол МОК, если МРК=800....

Популярные вопросы