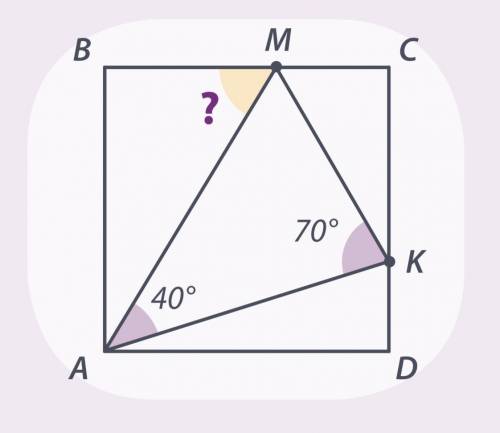
На сторонах ВС и СD квадрата АВСD взяли 24 точки М и К так, что угол КАМ равен 40°, а угол АКМ равен 70°. Найдите угол АМВ.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сөйлемдерде есімдіктің астын сыз олар шыршаны айналып,ән салып,би билейді.мен...
3 - Запел, звонкий, небе,в, жаворонок составить предложение...
3 - ответы должны быть полными и развернутыми (больше 3 предложений) организация...
3 - Как можно объяснить просхождение пемзы (кратко)?...
1 - Ничего в природе не могло быть лучше. синтаксический разбор предложения....
1 - Найти градусную меру rtf. варианты 86,94,274,133...
2 - Морфологический разбор слова заволочили...
3 - Однажды мальчик прочитал статью о тополях части речи разобрать...
1 - Турист шел со скоростью 100м/мин сколько километров турист за 10 мин? за 1ч.?...
1 - Изобразите на координатной плоскости множество решений неравенств с двумя переменными.!...
2
ответ: 65°
Объяснение:
очевидно, что уголАМК=70° (треугольник АМК -равнобедренный);
следовательно, прямоугольные треугольники АВМ и АDК равны по гипотенузе (АМ=АК) и катету (АВ=АD);
из этого следует, что ВМ=DК и следовательно СМ=СК,
т.е. прямоугольный треугольник СМК -равнобедренный и уголСМК=45°...
и тогда уголВМА=180°-70°-45°=65°...
или так: из равенства треугольников АВМ и АDК следует: уголМАВ = уголКАD = (90°-40°)/2 = 25°
и т.к. сумма острых углов прямоугольного треугольника равна 90°, то уголАМВ=90°-25°=65°