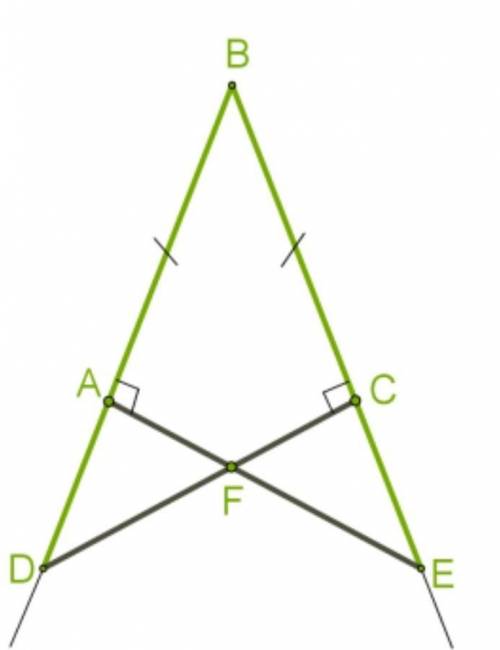
На сторонах угла ∡ ABC точки A и C находятся на равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥ BD, CD⊥ BE.  

1. Докажи равенство треугольников ΔAFD и ΔCFE.
BA=?=???

2. Определи величину угла, под которым перпендикуляр CD пересекает BA, если AE пересекает BC под углом 39°.

 

1. Назови треугольники, равенство которых позволит доказать равенство ΔAFD и ΔCFE:

ΔBA = Δ.?

 

По какому признаку доказывается это равенство?

По третьему
По второму
по третьему

 

Отметь элементы, равенство которых в этих треугольниках AFD CFE и позволяет применять выбранный признак:

 

углы                            стороны

FCE CE
CEF AD
DFA EF
ADF FA
EFC FC
FAD DF

1. Назови треугольники, равенство которых позволит доказать равенство ΔAFD и ΔCFE:

ΔBAЕ = ΔBCD

По какому признаку доказывается это равенство?

По второму

Отметь элементы, равенство которых в этих треугольниках позволяет применять выбранный признак:

углы

∠CBD = ∠ABE

иначе, ∠В - общий для этих треугольников.

∠EAB = ∠DCB

По условию AE⊥ BD, CD⊥ BE, значит эти углы равны 90°.

стороны

BC = BA

По какому признаку доказывается равенство ΔAFD и ΔCFE?

По второму

Отметь элементы, равенство которых в треугольниках ΔAFD и ΔCFE позволяет применять выбранный признак:

углы

∠FAD = ∠FCE

так как эти углы прямые

∠CEF = ∠ADF

из равенства треугольников ΔBAЕ и ΔBCD.

стороны

AD = CE

AD = BD - BA, CE = BE - BC

BD = BE из равенства треугольников ΔBAЕ и ΔBCD, ВА = ВС по условию, значит AD = CE.

2. Величина угла, под которым перпендикуляр CD пересекает прямую BA — 71°

Угол, под которым CD пересекает ВА, - это ∠ADF.

Угол, под которым АЕ пересекает ВС, - это ∠СЕF, по условию ∠CEF = 71°.

∠ADF = ∠CEF = 71° из равенства треугольников AFD и CFE.