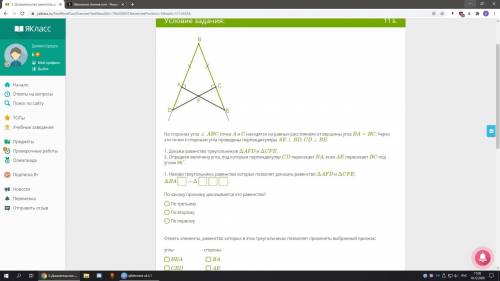
На сторонах угла ∡ ABC точки A и C находятся на равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥ BD, CD⊥ BE. 1. Докажи равенство треугольников ΔAFD и ΔCFE.
2. Определи величину угла, под которым перпендикуляр CD пересекает BA, если AE пересекает BC под углом 80°.

1. Назови треугольники, равенство которых позволит доказать равенство ΔAFD и ΔCFE:
ΔBA
= Δ
.

По какому признаку доказывается это равенство?
По третьему
По второму
По первому

Добрый день! Давайте рассмотрим по порядку каждый из вопросов.

1. Чтобы доказать равенство треугольников ΔAFD и ΔCFE, нам необходимо найти равные стороны и равные углы этих треугольников.

Первым шагом рассмотрим равенство сторон. У нас есть утверждение, что точки A и C находятся на равных расстояниях от вершины угла ∡ABC. В этом случае, можно сказать, что стороны AD и CF равны по длине.

Вторым шагом рассмотрим равенство углов. Мы видим, что угол ∡DAF и угол ∡CEF - это прямые углы, так как AD и CF являются перпендикулярами к сторонам BC и AB, соответственно. Значит, эти углы равны между собой.

Теперь мы имеем равные стороны AD = CF и равные углы ∡DAF = ∡CEF. По третьему признаку равенства треугольников, мы можем сделать вывод, что треугольники ΔAFD и ΔCFE равны.

2. Чтобы определить величину угла, под которым перпендикуляр CD пересекает BA, если AE пересекает BC под углом 80°, мы должны воспользоваться свойствами перпендикуляров и свойствами углов.

Мы знаем, что перпендикуляр создает прямой угол с той стороной, к которой он проведен. Значит, угол ∡BCD = 90°. Также, угол ∡BAE = 80°, по условию. Мы знаем, что сумма углов треугольника равна 180°. Следовательно, угол ∡EAB = 180° - 90° - 80° = 10°.

Таким образом, мы определили, что перпендикуляр CD пересекает сторону BA под углом 10°.

Итак, для своевременного заключения: треугольники ΔAFD и ΔCFE равны по третьему признаку равенства, а угол, под которым перпендикуляр CD пересекает BA, равен 10°.