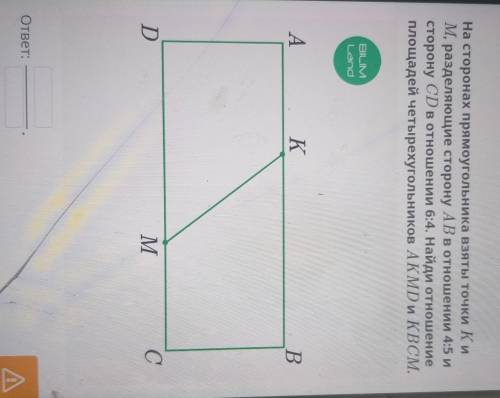
На сторонах прямоугольника взяты точки Ки M, разделяющие сторону ABв отношении 4:5 и сторону CD в отношении 6:4. Найди отношение площадей четырехугольников AKMD и КВСМ.
Другие вопросы по теме Геометрия
Популярные вопросы
- 7. Для пловцов купили 138 халата и 230 плавок. Найдите возможное...
2 - «Сауда жасай білесің бе?» тақырыбына эссе жазасыңдар. 150 сөзден...
2 - YbyralAltynsarin Ybyrai Ibrahim) Altynsarin (1841 - 1889) was...
3 - .Основная причина поражения казахов от джунгар A. недостаточный...
3 - из данного и позы Найди и подчеркни предложение выражения главные...
3 - 5. Теңдеуді шешiiп, тексеріңіз.2(у - 5)+14=26...
1 - Запишите предложения используя глаголь в нужнойформе пассивного...
1 - Привезенные в школу тетради необходимо поровну без остатка распределить...
1 - 1. (1,5б). Точка М належить відрізку AB. Знайдіть довжину відрізка...
1 - нужно 1. We are going to take a guided/reality tour of a museum...
1
Вот так вот
Объяснение:
AlexUnderNewSky
AK=4x, KB=5x, AB=9x
DM=6y, MC=4y, DC=10y
Противоположные стороны прямоугольника равны.
AB=DC => 9x=10y => y=0,9x
AKMD и KBCM - прямоугольные трапеции, AD=BC - высоты
S(AKMD) =1/2 (AK+DM) AD
S(KBCM) =1/2 (KB+MC) BC
S(AKMD)/S(KBCM) =(AK+DM)/(KB+MC) =
= (4x+6y)/(5x+4y) = (4x+6*0,9x)/(5x+4*0,9x) =9,4x/8,6x =47/43