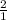на сторонах bc и cd параллелограмма abcd отметили соответственно точки F и E так , что BF:FC= 0,5 , DE: EC=0,75.Прямые FD и AE пересекаются в точке M.Найдите отношение FM:MD
Другие вопросы по теме Геометрия
Популярные вопросы
- Стороны одного четырехугольника относятся как 3 : 5: 7: 11 а суммарная...
2 - Нужно отследить и нарисовать график функции : y(х)=3x^2+8х-4...
1 - Докажите, что выражение может принимать лишь отрицательные значения....
1 - 6слов с двумя безударными гласными е в корне слова?...
2 - Можно доп. материал по 2-м темам. на 1 страницу примерно. 1. места обитания...
1 - Какие памятники и культуры есть в перми?...
2 - Прочитай и запиши её решение ..в четырех круглых корзинах по 9 кг яблок...
1 - Нужно написать сочинение-описание морской свинки( у меня мальчик черной...
3 - Масса шести ящиков с яблоками равна 72кг .масса пустого ящика равна 3кг....
2 - ((а+в)+с)2степени ((а-в)-с)2степени (3х-0,2в+у)2степени (0,7х+5в4ст.-0,2а5ст.)...
1
Объяснение: см. во вложении
на сторонах bc и cd параллелограмма abcd отметили соответственно точки F и E так , что BF:FC= 0,5 , DE: EC=0,75.Прямые FD и AE пересекаются в точке M.Найдите отношение FM:MD
Объяснение:
BF:FC= 1/2 , DE: EC=3/4.
Пусть ВС=а, DC=в. Тогда FC=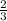 a
a
1) ΔFMY ≈ΔDMA по двум вертикальным углам и накрест лежащем при ВС║AD, AY-секущая : ∠FMY=DMA , ∠FYM=∠DAM.
В подобных треугольниках сходственные стороны пропорциональны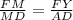 или
или 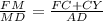 .
.
2) ΔCEY ≈ΔDEA по двум вертикальным углам и накрест лежащем :при ВС║AD, AY-секущая : ∠СEY=DEA , ∠CYE=∠EAD.
В подобных треугольниках сходственные стороны пропорциональны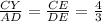 или CY=
или CY=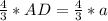
3)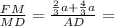
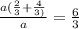 =
=