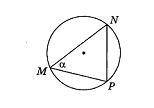
На рисунке треугольник MNP вписан в окружность. Найдите радиус окружности, если известно, что угол MNP=a NP=5

Для решения этой задачи мы воспользуемся свойствами вписанного угла и длинами сторон треугольника.

Когда треугольник вписан в окружность, сумма углов треугольника, образованных наибольшей стороной и дугой окружности, равна 180 градусов. В нашей задаче, угол MNP является вписанным углом, поскольку его вершина находится на окружности, и NP является дугой окружности. Поэтому мы можем выразить эту сумму углов следующим образом:

угол MNP + угол NMP = 180 градусов

В данной задаче у нас известно, что угол MNP равен a градусам, поэтому мы можем записать:

a + угол NMP = 180 градусов

Также у нас есть информация о длине стороны NP, которая равна 5.

Так как треугольник MNP является прямоугольным, мы можем использовать теорему Пифагора для нахождения длин сторон. В данном случае, сторона MN является гипотенузой, а стороны MP и NP являются катетами. Поэтому мы можем записать:

MN^2 = MP^2 + NP^2

Поскольку у нас есть информация о длине стороны NP и она равна 5, мы можем записать:

MN^2 = MP^2 + 5^2

Теперь мы можем выполнять следующие шаги для решения задачи:

1. a + угол NMP = 180 градусов
Решим уравнение относительно угла NMP: угол NMP = 180 - a

2. MN^2 = MP^2 + 5^2
Выразим MP^2: MP^2 = MN^2 - 25

3. Подставим выражение для угла NMP в уравнение для длин стороны MN:
MN^2 = (MN^2 - 25) + 5^2

4. Решим полученное уравнение для длины стороны MN:
MN^2 = MN^2 - 25 + 25
0 = 0

Это тривиальное уравнение означает, что решений нет, и оно нам говорит о том, что такого треугольника невозможно построить.

Итак, радиус окружности не может быть определен в данной задаче, так как такого треугольника не существует.