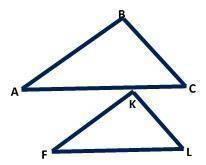
На рисунке представлены два подобных треугольника. Угол C первого равен углу L второго и составляет 650. Сторона AC первого 19,5 см, а сторона FL второго равна 13,0 см. При этом сторона BC первого = 12,0 см, а сторона FK второго = 12,0 см. Найдите длины стороны AB первого и KL второго.
Другие вопросы по теме Геометрия
Популярные вопросы
- Рассмотрите таблицу не и ни в отрицательных местоимениях и наречиях...
3 - Как написать ну ты чего заснула чтоле со всеми знаками препинания...
3 - Свыбором sometimes i wonder if i _ ever succeed. 1. do 2. shall 3....
3 - Из данных линейных функций выберите ту,которая является прямой пропорциональностью...
2 - Найти натуральное решение ( n+299)*(n-200)=2014...
3 - Начертите таблицу не с существительными,прилагательными и наречиями...
3 - Сделать правильный выбор before you telephoned, i _ watching television....
3 - Медную деталь,нагретую до 720°c,погрузили в 1,75кг воды при температуре...
2 - Втриугольнику авс на стороне ав взяли точку м так, что ам: вм=2:...
3 - ;какая из этих реакций не является окислительно-восстановительной?...
3
Для начала, мы можем найти отношение длин сторон AB первого треугольника и KL второго треугольника. Для этого используем отношение длин сходных сторон:
AB/KL = AC/FL
Подставим известные значения:
AB/KL = 19,5/13,0
Теперь найдем значение AB. Для этого умножим обе части уравнения на KL:
AB = (19,5/13,0) * KL
Теперь мы знаем, что AB равно (19,5/13,0) умножить на KL. Осталось только найти KL.
По условию задачи угол C первого треугольника равен углу L второго треугольника и составляет 650. Это значит, что угол C в первом треугольнике и угол L во втором треугольнике являются прямыми углами.
Таким образом, у нас есть два прямых угла, а сумма углов в треугольнике равна 180 градусов. Значит, третий угол в первом треугольнике будет равен 180 минус 90 минус 650:
Угол A в первом треугольнике = 180 - 90 - 65 = 25 градусов.
Теперь мы знаем, что угол A в первом треугольнике равен 25 градусам, а угол C равен 90 градусам. Мы также знаем, что сторона BC равна 12,0 см.
Можно воспользоваться синусом угла A и сторонами треугольника для нахождения стороны AB.
sin A = противолежащая сторона / гипотенуза
sin 25 = AB / 12,0
Теперь мы можем найти значение AB, умножив обе части уравнения на 12,0:
AB = sin 25 * 12,0
Таким образом, мы можем найти длины сторон AB первого и KL второго треугольников.